Неравенство Чебышева

Получим вначале некоторые оценки для распределений СВ.

Лемма. Если неотрицательная СВ имеет конечное математическое ожидание 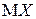, то для любого 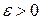справедливо неравенство:

.

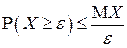▲ Докажем лемму для НСВ (для ДСВ доказать самостоятельно). По определению математического ожидания НСВ

■.

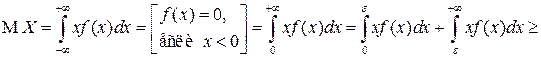
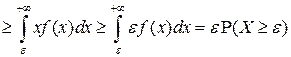Следствие (неравенство Чебышева). Если СВ имеет конечную дисперсию 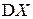, то для любого 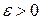справедливы следующие неравенства:

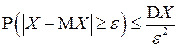;(4.15)

.

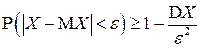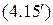
▲В соответствии с леммой

,

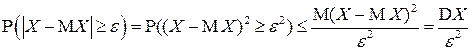что доказывает неравенство (4.15). Неравенство 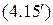следует из (4.15) путем перехода к противоположному событию ■.

Неравенство Чебышева имеет большое теоретическое и практическое значение. Оно дает простую оценку для вероятности отклонения СВ с произвольным ЗР от ее математического ожидания. Причем, если о СВ, кроме ее математического ожидания и дисперсии ничего не известно, то эту оценку улучшить нельзя (существует пример СВ, для которой в (4.15) достигается равенство). Если же есть дополнительная информация о СВ (например, известен ее ЗР), то оценки (4.15) и 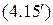могут быть существенно улучшены.

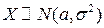Пример. Пусть СВ имеет нормальный ЗР: . Тогда:

- на основании неравенства Чебышева

;

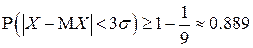- в соответствии с «правилом »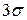

,

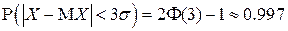где 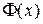- функция Лапласа.