2015-02-14
4893
Пусть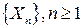 
- последовательность независимых одинаково распределенных СВ с конечной дисперсией 
, 
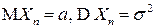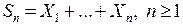- сумма первых 
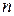СВ.
В соответствии с ЗБЧ (Теорема 3)
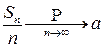
или, после приведения к общему знаменателю,
.
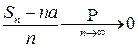Возникает вопрос: если при делении на 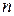мы получили в пределе 0 (в смысле некоторой, все равно какой, сходимости), то не слишком ли на «много» мы поделили? Нельзя ли поделить на что-нибудь, растущее к 
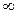медленнее, чем 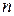, чтобы получить в пределе не 0 (и не 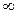, естественно)?Оказывается, что уже последовательность СВ 
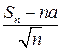сходится не к 0, а к СВ, причем имеющей нормальный ЗР!
Теоремы, которые устанавливают нормальность предельного закона распределения суммы СВ называются центральными предельными теоремами (ЦПТ). Мы ограничимся приведением формулировок только двух таких теорем, которые касаются сумм независимых СВ (доказательства этих теорем основаны на использовании аппарата характеристических функций, выходящего за рамки данного курса, и потому приводиться не будут).
Теорема 1 (ЦПТ для независимых, одинаково распределенных СВ).
|
|
|
Пусть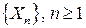 
- последовательность независимых, одинаково распределенных случайных величин, имеющих конечное математическое ожидание 
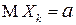и дисперсию 
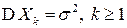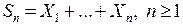, - сумма первых 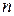СВ.
Тогда при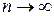 
равномерно по всем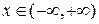 
.
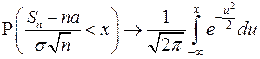Учитывая, что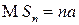 
, а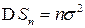 
, утверждение теоремы можно переписать в виде:
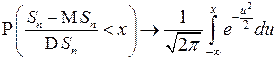
или
,
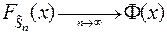где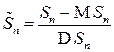 
- центрированная и нормированная сумма СВ (
, 
); 
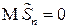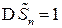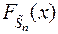- ФР суммы 
; 
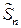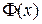- ФР стандартного нормального закона распределения 
.
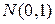Таким образом, стремление ЗР суммы СВ к нормальному ЗР следует понимать в смысле сходимости при 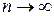ФР СВ 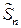к ФР СВ 
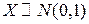равномерно по всем значениям аргумента.
Условия сходимости ФР суммы независимых разнораспределенных слагаемых к ФР стандартного нормального ЗР содержится в следующей теореме, принадлежащей А.М. Ляпунову.
Теорема 2 (Ляпунова) (ЦПТ для независимых, разнораспределенных СВ)
Пусть 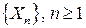- последовательность независимых разно-распределенных СВ, имеющих конечные математические ожидания 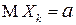,дисперсии 
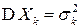и центральные абсолютные моменты 
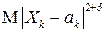порядка 
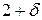при некотором 
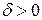и любом 
.
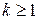Обозначим 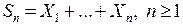- сумму первых 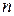СВ, 
, 
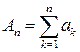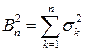и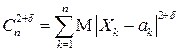 
.
Тогда, если
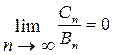(условие Ляпунова),
то при 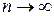равномерно по всем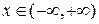
.
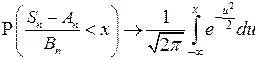или
,
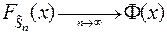где 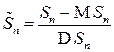- центрированная и нормированная сумма СВ; 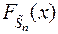- ФР суммы 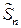; 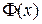- ФР стандартного нормального закона распределения .
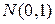Выясним вероятностный смысл условия Ляпунова.
Для этого рассмотрим при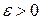 
события 
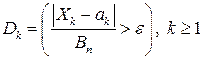. Тогда 
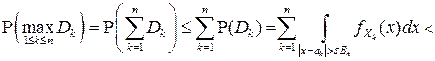
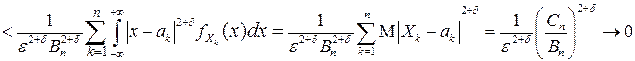
при 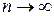, если условие Ляпунова выполнено.
Таким образом, если условие Ляпунова выполняется, то все слагаемые в центрированной и нормированной сумме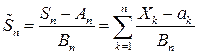 
равномерно малы в том смысле, что вероятность хотя бы одному из них превзойти величину 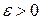стремится к нулю при возрастании числа слагаемых. Другими словами, влияние каждого слагаемого на всю сумму должно быть очень мало, для того, чтобы ЦПТ имела место. (Заметим, что это касается только случая разнораспределенных слагаемых, для одинаково распределенных слагаемых ЦПТ выполняется без каких-либо дополнительных предположений).
|
|
|
При ссылках на ЦПТ удобно использовать понятие асимптотической нормальности.
Определение. Говорят, что СВ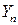 
при 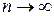асимптотически нормальна с параметрами 
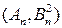(краткая запись: 
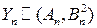), если ФР СВ 
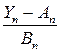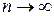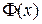сходится при к ФР стандартного нормального ЗР равномерно по всем .
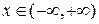С учетом этого определения утверждения Теорем 1 и 2 можно записать следующим образом.
Теорема 1.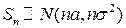 
; Теорема 2.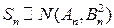 
Прикладное значение ЦПТ состоит в следующем. Если СВ представляет собой сумму большого числа независимых СВ, то можно считать, что ее ЗР является нормальным, причем тип распределения слагаемых безразличен. Этим фактом и обусловлено широкое распространение на практике нормального ЗР.
Проиллюстрируем действие ЦПТ на сумме независимых,равномерно распределенных СВ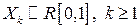 
.
Обозначим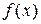 
- ПВ СВ 
, , 
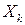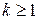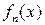- ПВ СВ 
.
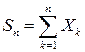С одной стороны, ПВ 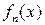можно найти аналитически с помощью интеграла свертки (4.13):
.
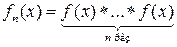Графическая иллюстрация этого:
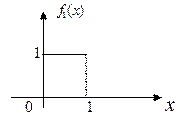
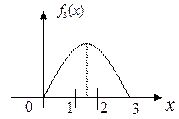
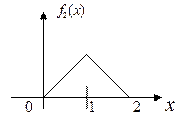
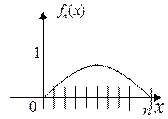С другой стороны, поскольку 
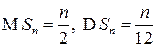, то в соответствии с ЦПТ СВ
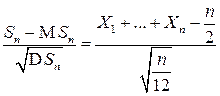
имеет приблизительно нормальный ЗР с параметрами (0,1) или, что эквивалентно, СВ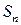 
является асимптотически нормальной: 
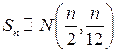. Последнее означает, что для ПВ 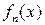справедливо приближенное равенство:
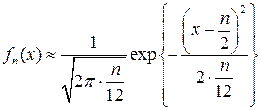. (4.19)
Оказывается, что уже при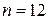 
, точность приближения в равенстве (4.19) вполне пригодна для практического использования и это свидетельствует о достаточно быстрой скорости сходимости в ЦПТ.
При 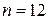утверждение ЦПТ принимает вид:
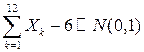. (4.20)
На последнем соотношении основан алгоритм получения значений стандартной нормальной СВ 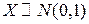с помощью значений СВ 
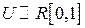, то есть с помощью датчика случайных чисел:
.
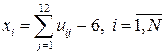Заметим, что алгоритм моделирования стандартной нормальной СВ с помощью функции, обратной к ФР, неприменим, поскольку функция Лапласа 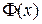не выражается через элементарные.
