Функции от случайных величин

Дискретный случай. Пусть – ДСВ, принимающая значения 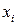с вероятностями 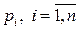(случай счетного числа значений СВ рассмотреть самостоятельно). Тогда для произвольной неслучайной функции 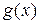, область определения которой содержит множество возможных значений СВ , СВ 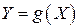является дискретной и задача состоит в нахождении ее ЗР.

а) Предположим вначале, что все значения 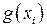различны (так, в частности, может быть, если функция 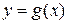является монотонной в области возможных значений случайной величины ). Тогда случайная величина 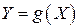будет иметь столько же возможных значений 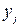, как и случайная величина , с 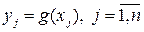и при этом

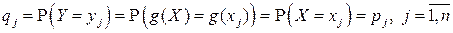. (4.1)

Таким образом, ЗР СВ 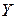имеет вид:

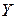
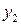
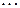
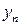
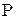
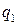
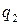
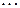
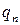
где в соответствии с (4.1) вероятность .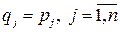

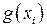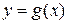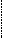
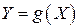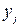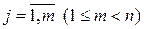б) Предположим теперь, что среди значений есть совпадающие (это может быть, в частности, если функция не является монотонной в области возможных значений случайной величины ). Тогда случайная величина будет иметь меньше возможных значений, чем случайная величина , и ими являются , , различные среди 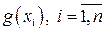. При этом вероятности 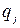значений 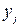определяются по формуле:

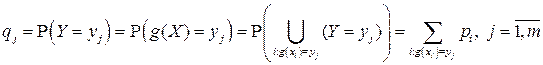, (4.2)

ЗР СВ 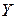в данном случае имеет вид:

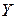
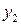
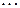
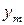
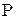
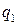
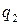
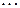
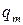
где в соответствии с (4.2) вероятности 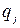являются суммой вероятностей 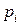тех значений 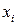, для которых . , .

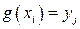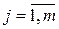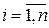Пример. Найти ЗР СВ 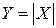, если СВ Х является дискретной и имеет ЗР

	-2	-1
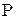
	0.2	0.2	0.2	0.2	0.2

Решение. В соответствии с (4.2) ЗР СВ 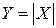имеет вид:

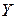
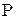
	0.2	0.4	0.4

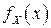Непрерывный случай. Если – НСВ с ПВ , а 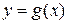– дифференцируемая функция в области возможных значений случайной величины Х. Тогда величина 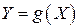является непрерывной СВ и задача состоит в нахождение ПВ .

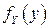Предположим вначале, что 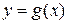- монотонно возрастающая функция в области возможных значений СВ Х. Тогда у функции 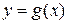существует однозначная обратная функция 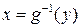и ФР СВ 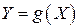можно записать в виде:

.

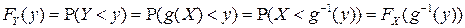Дифференцируя обе части полученного равенства по 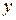, получаем:

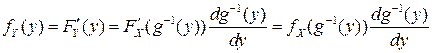. (4.3)

Для монотонно убывающей в области возможных значений СВ Х функции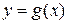

,

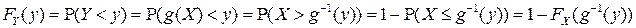а после дифференцирования по 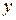обеих частей этого равенства

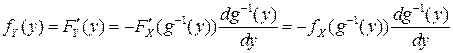. (4.4)

Объединяя полученные в (4.3) и (4.4) результаты, получаем:

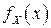Если – НСВ с ПВ , а 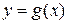– монотонная дифференцируемая функция, то СВ 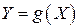является непрерывной и ееПВ 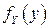определяется через 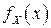по формуле:

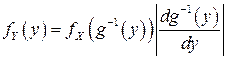, (4.5)

где 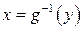– функция, обратная к функции 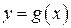(отметим, что равенство (4.5) имеет место в точках непрерывности ПВ 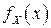и ).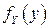

Если дифференцируемая функция 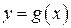не является монотонной в области

возможных значений случайной величины , то ее область определения можно разбить на 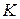непересекающихся интервалов, на каждом из которых она монотонной будет и будет иметь однозначную обратную функцию 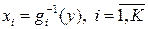. Применяя формулу (4.5) на каждом интервале монотонности, получаем:

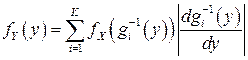. (4.6)

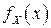Пример 1. Пусть – НСВ с ПВ , а 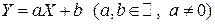. Найти ПВ .

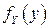Решение. В данном случае функция 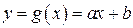является монотонной при любых значениях 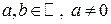(при 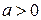функция 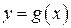возрастает, при 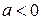- убывает). Функция, обратная к 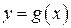, имеет вид:

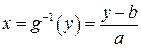, а ее производная 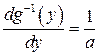. Поэтому в соответствии с (4.5)

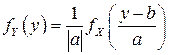. (4.7)

а) Рассмотрим линейное преобразование вида 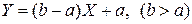над СВ .

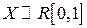В соответствии с (4.7) в этом случае 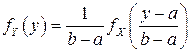, а с учетом того, что

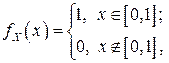
для ПВ СВ 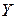имеем выражение:

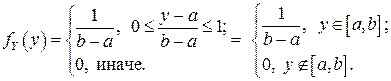
Полученный результат схематично можно записать

.

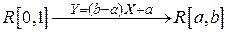и он означает, что из равномерного распределения на отрезке 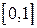можно получить равномерное распределение на любом отрезке 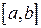путем линейного преобразования.

б) Рассмотрим линейное преобразование вида 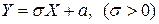над СВ .

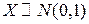В соответствии с (4.7) в этом случае 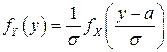, а с учетом того, что

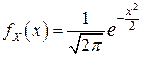
для ПВ СВ 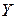имеем выражение:

.

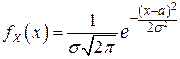Полученный результат схематично можно записать

.

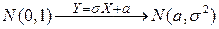и он означает, что из стандартного нормального распределения можно получить нормальное распределение с любыми параметрами 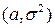путем линейного преобразования.

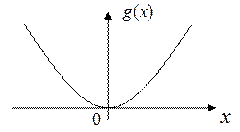Пример 2. Пусть 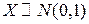, а 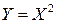. Найти плотность вероятностей .

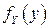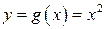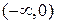Решение. В данном случае функция не является монотонной в области возможных значений случайной величины и имеет два интервала монотонности и 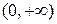. На каждом из интервалов функция 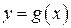имеет однозначную обратную функцию: 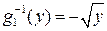на первом интервале 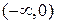и 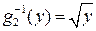- на втором 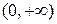. Поскольку модуль производной 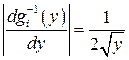, , 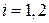то в соответствии с (4.6)

,

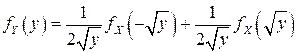а с учетом того, что 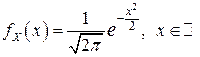, получаем:

,

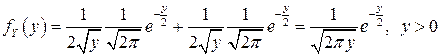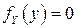при .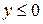

Пример 3. Пусть 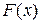- строго монотонная ФР, а СВ 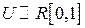. Тогда СВ 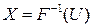имеет заданную ФР .

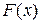Решение. Действительно,

.

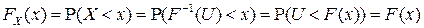Последнее равенство следует из того, что ФР СВ 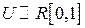имеет вид:

.

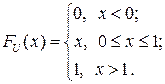Смысл примера 3. Предположим, что требуется получить 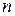значений 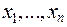СВ с заданным ЗР (смоделировать СВ ). Для этого в соответствии с примером 3 необходимо найти ФР 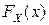СВ и, если она имеет однозначную обратную функцию, то положить

, ,

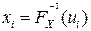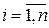где 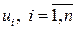- значения СВ, имеющей равномерное распределение на отрезке 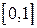(значения 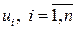можно получитьпутем обращения к датчику случайных чисел, входящему в стандартное математическое обеспечение любого персонального компьютера).