Часто на практике возникает задача определения ЗРСВ 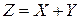 , являющейся суммой координат
, являющейся суммой координат 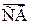
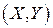 . Если при этом одну из СВ интерпретировать как полезный сигнал, а вторую СВ как шум, то в приложениях эта задача известна как исследование модели «сигнал + шум».
. Если при этом одну из СВ интерпретировать как полезный сигнал, а вторую СВ как шум, то в приложениях эта задача известна как исследование модели «сигнал + шум».
Применяя формулы (4.8) и (4.9) для функции 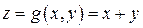 получаем следующие результаты.
получаем следующие результаты.
Если 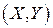 -
- 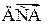 , принимающий конечное число значений
, принимающий конечное число значений 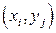 с вероятностями
с вероятностями 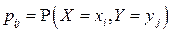 ,
, 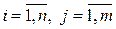 , то
, то 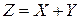 – ДСВ и ее возможными значениями
– ДСВ и ее возможными значениями 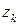 ,
, 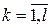 , являются различные среди значений
, являются различные среди значений 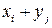 . Вероятности значений
. Вероятности значений 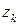 определяются по формуле:
определяются по формуле:
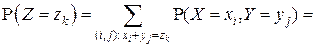
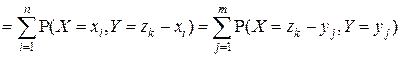 ,
, 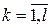 (4.10)
(4.10)
(при этом предполагается, что вероятность 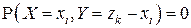 , если
, если 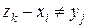 ни при каком j, и аналогично вероятность
ни при каком j, и аналогично вероятность 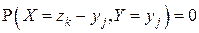 , если
, если 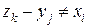 ни при каком i).
ни при каком i).
Если 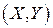 -
- 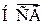 сПВ
сПВ 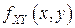 , то СВ
, то СВ 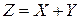 является непрерывной и ФР
является непрерывной и ФР 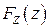 СВ
СВ 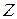 имеет вид:
имеет вид:
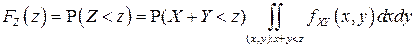
а, после расстановки пределов по области 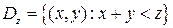 ,
,
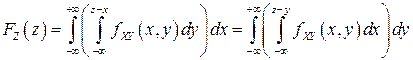
Дифференцируя обе части последнего равенства по 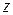 , получаем:
, получаем:
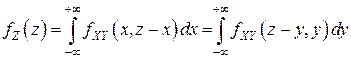 (4.11)
(4.11)
(в точках непрерывности ПВ 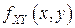 ,
, 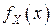 и
и 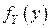 ).
).
Если дополнительно известно, что координаты 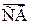
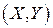 являются независимыми СВ, то:
являются независимыми СВ, то:
· СВ 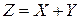 является дискретной, если
является дискретной, если  и
и 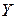 - ДСВ, и имеет ЗР, определяемый в соответствии с (4.10) вероятностями:
- ДСВ, и имеет ЗР, определяемый в соответствии с (4.10) вероятностями:
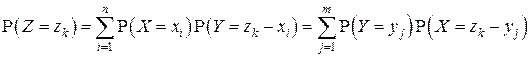 ,
, 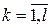 (4.12)
(4.12)
(при этом предполагается, что вероятность 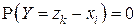 , если
, если 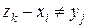 ни при каком j, и аналогично вероятность
ни при каком j, и аналогично вероятность 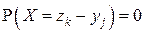 , если
, если 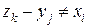 ни при каком i).
ни при каком i).
· СВ 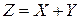 является непрерывной, если
является непрерывной, если  и
и 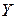 - НСВ, и имеет в соответствии с (4.11) ПВ:
- НСВ, и имеет в соответствии с (4.11) ПВ:
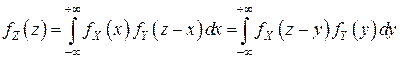 , (4.13)
, (4.13)
где 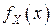 и
и 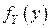 - ПВСВ
- ПВСВ  и
и 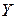 соответственно;
соответственно;
· СВ 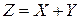 является непрерывной, если
является непрерывной, если  - дискретная а
- дискретная а 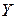 - непрерывная СВ, и имеет ПВ:
- непрерывная СВ, и имеет ПВ:
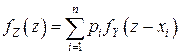 , (4.14)
, (4.14)
где 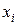 и
и 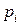 ,
, 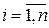 - значения СВ
- значения СВ  и соответствующие им вероятности, а
и соответствующие им вероятности, а 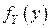 - ПВ СВ
- ПВ СВ 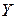 .
.
Получается данныйрезультат комбинированием дискретного и непрерывного случаев. Вначале находится ФР НСВ 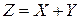 с учетом независимости СВ
с учетом независимости СВ  и
и 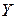 :
:
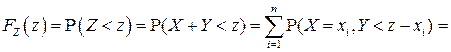
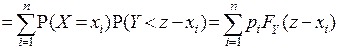 ,
,
а затем дифференцированием 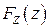 по
по 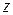 получаем для ПВ
получаем для ПВ 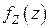 выражение (4.14).
выражение (4.14).
Задача определения ЗР суммы независимых СВпо ЗР слагаемых в теории вероятностей называется задачей композиции ЗР, а в функциональном анализе – сверткой функций. По этой причине формулу (4.13) кратко можно записать в виде 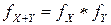 (где
(где 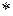 означает операцию свертки), а интегралы в ней называют интегралами свертки.
означает операцию свертки), а интегралы в ней называют интегралами свертки.
Замечание. Все результаты, полученные для двумерного СВ, без труда обобщаются и на многомерный случай.
Пример. Пусть 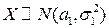 ,
, 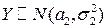 и СВ
и СВ  и
и 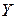 независимы. Найти ПВ СВ
независимы. Найти ПВ СВ 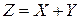 .
.
Решение. Для простоты положим 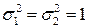 (общий случай рассмотреть самостоятельно).Тогда, в соответствии с интегралом свертки (4.13), имеем:
(общий случай рассмотреть самостоятельно).Тогда, в соответствии с интегралом свертки (4.13), имеем:
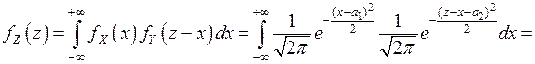
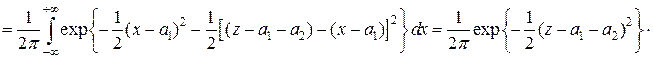
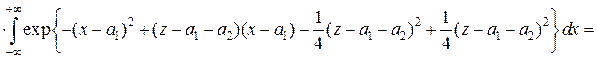
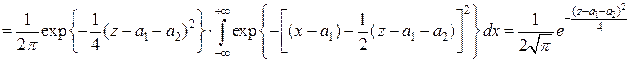
(при этом был использован тот факт, что 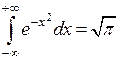 - интеграл Пуассона)
- интеграл Пуассона)
Таким образом, СВ 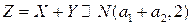 .
.
В общем случае, когда 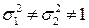 , СВ
, СВ 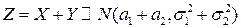 .
.
По индукции можно доказать, что если СВ 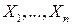 независимы (в совокупности) и
независимы (в совокупности) и 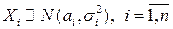 , то СВ их любая линейная комбинация также имеет нормальный ЗР:
, то СВ их любая линейная комбинация также имеет нормальный ЗР:
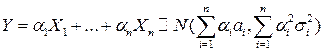 .
.
 2015-02-14
2015-02-14 1605
1605








