2015-02-14
3614
Определение. Говорят, что последовательность СВ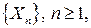 
сходится по вероятности к величине 
(случайной или нет), если для любого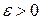 
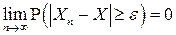
или, что эквивалентно,
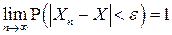
Краткое обозначение сходимости по вероятности: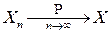 
.
Определение. Говорят, что последовательность СВ 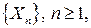сходится в среднем квадратическом к величине (случайной или нет), если
.
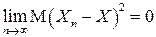Краткое обозначение сходимости в среднем квадратическом: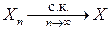 
или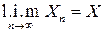 
(limitinthemean).
Лемма. Если последовательность СВ 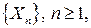сходится к величине в среднем квадратическом, то она сходится к этой величине и по вероятности:
.
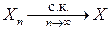
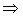
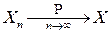▲ В силу неравенства Чебышева
.
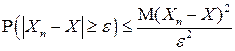Поэтому, если 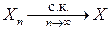, то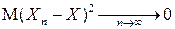 
и, следовательно, для любого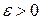 
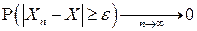, поскольку вероятность не может быть отрицательной (лемма о двух милиционерах)■.
Смысл леммы: сходимость в среднем квадратическом является более сильной, чем сходимость по вероятности. Обратное неверно: из сходимости по вероятности сходимость в среднем квадратическом не следует.
Смысл введенных видов сходимостей последовательностей СВ: понятие предела определено только для числовой последовательности, поэтому случайность под знаком предела должна быть ликвидирована. Это делается либо с помощью вероятности, либо с помощью математического ожидания со своим понятием близости между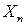 
и .
|
|
|
