Пусть 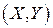 – двумерный
– двумерный  с заданным ЗР и СВ
с заданным ЗР и СВ 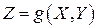 , где
, где 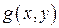 – неслучайная скалярная функция двух переменных, область определения которой содержит множество возможных значений вектора
– неслучайная скалярная функция двух переменных, область определения которой содержит множество возможных значений вектора 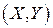 . Рассмотрим задачу нахождения ЗР СВ
. Рассмотрим задачу нахождения ЗР СВ 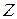 .
.
Пусть 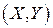 –
– 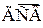 , принимающий конечное число значений
, принимающий конечное число значений 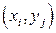 с вероятностями
с вероятностями 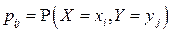 ,
,  (случай счетного числа значений
(случай счетного числа значений  рассмотреть самостоятельно). Тогда
рассмотреть самостоятельно). Тогда 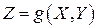 – ДСВ и ее возможными значениями
– ДСВ и ее возможными значениями 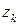 ,
, 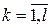 являются различные среди значений
являются различные среди значений 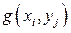 (
(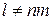 может быть). При этом вероятности значений
может быть). При этом вероятности значений 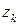 аналогично одномерному случаю определяются по формуле:
аналогично одномерному случаю определяются по формуле:
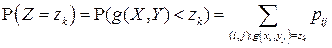 ,
, 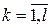 . (4.8)
. (4.8)
Если 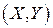 –
– 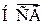 с ПВ
с ПВ 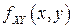 , то
, то 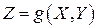 является НСВ, если функция
является НСВ, если функция 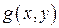 дифференцируема по каждому из своих аргументов. При этом ФР
дифференцируема по каждому из своих аргументов. При этом ФР 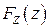 СВ
СВ 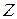 определяется формулой:
определяется формулой:
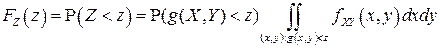 , (4.9)
, (4.9)
а ПВ 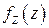 находится дифференцированием
находится дифференцированием 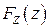 по
по 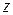 .
.
 2015-02-14
2015-02-14 283
283








