Функция, непрерывная на замкнутом ограниченном множестве, является равномерно непрерывной.
Пример 1. Доказать, что функция 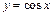 равномерно непрерывна на
равномерно непрерывна на 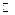 .
.
Для 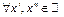 имеем:
имеем: 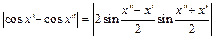 . Используя неравенства
. Используя неравенства 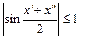 и
и 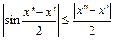 , если
, если 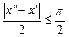 , получим:
, получим: 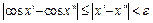 , если
, если 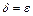 . Таким образом, для
. Таким образом, для 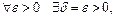 что для
что для 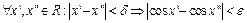 , т.е. функция
, т.е. функция 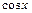 равномерно непрерывна на
равномерно непрерывна на 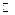 .
.
Пример 2. Цех завода вырабатывает квадратные пластинки, стороны которых 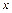 могут принимать значения в пределах от 1 до 10 см. С каким допуском
могут принимать значения в пределах от 1 до 10 см. С каким допуском 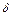 можно обрабатывать стороны этих пластинок, чтобы независимо от их длины (в указанных границах) площадь их
можно обрабатывать стороны этих пластинок, чтобы независимо от их длины (в указанных границах) площадь их 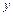 отличалась от проектной меньше, чем на
отличалась от проектной меньше, чем на 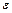 ? Произвести численный расчет, если а)
? Произвести численный расчет, если а) 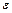 = 1см2; б)
= 1см2; б) 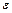 = 0,01см2; в)
= 0,01см2; в) 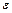 = 0,0001см2.
= 0,0001см2.
Площадь квадратной пластины со стороной 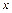 равна
равна 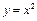 . Поэтому задача состоит в исследовании на равномерную непрерывность функции
. Поэтому задача состоит в исследовании на равномерную непрерывность функции 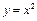 на множестве [1,10].
на множестве [1,10].
Рассмотрим разность: 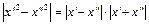 . На рассматриваемом промежутке сумма
. На рассматриваемом промежутке сумма 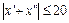 , следовательно,
, следовательно, 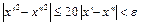 , откуда
, откуда 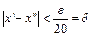 . Таким образом, для
. Таким образом, для 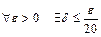 , что для
, что для 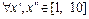 из условия
из условия  следует
следует 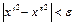 .
.
Произведем вычисления: а) если 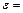 1см2, то
1см2, то 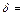 1/20=0,05см; б) если
1/20=0,05см; б) если 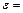 0,01см2, то
0,01см2, то 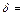 0,0005см; в) если
0,0005см; в) если 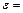 0,0001см2, то
0,0001см2, то 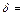 0,000005см.
0,000005см.
Пример 3. В положительном смысле сформулируйте на языке “ 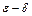 ” утверждение: функция
” утверждение: функция 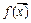 , непрерывная на некотором множестве (интервале, сегменте), не является равномерно непрерывной на этом множестве.
, непрерывная на некотором множестве (интервале, сегменте), не является равномерно непрерывной на этом множестве.
Пусть функция непрерывна на множестве 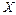 , по определению непрерывности это означает, что функция непрерывна в любой точке этого множества:
, по определению непрерывности это означает, что функция непрерывна в любой точке этого множества: 
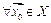 выполнено условие -
выполнено условие - 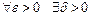 такое, что
такое, что 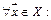
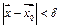 имеет место неравенство
имеет место неравенство 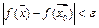 . Итак, зафиксировав произвольное
. Итак, зафиксировав произвольное 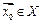 , мы по любому выбранному
, мы по любому выбранному 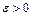 указываем
указываем 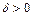 , т.е.
, т.е. 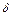 будет зависеть и от
будет зависеть и от 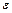 , и от
, и от 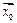 . В определении же равномерной непрерывности по
. В определении же равномерной непрерывности по 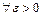 указывается
указывается 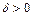 , которое годится для всех
, которое годится для всех 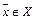 одновременно. Если же функция
одновременно. Если же функция 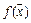 не является равномерно непрерывной на
не является равномерно непрерывной на 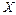 , это означает, что:
, это означает, что: 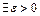
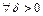
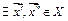 и такие, что
и такие, что 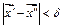 , но при этом
, но при этом 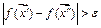 .
.
Пример 4. Исследовать на равномерную непрерывность функцию 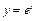 на
на 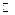 .
.
Рассмотрим разность 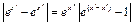 . Положим
. Положим 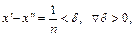 тогда
тогда 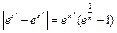 .
.
Пусть 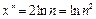 и
и 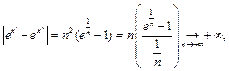 т.к.
т.к. 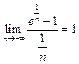 . Следовательно, функция
. Следовательно, функция 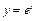 не является равномерно непрерывной на
не является равномерно непрерывной на 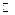 .
.
Пример 5. Исследовать на равномерную непрерывность функцию 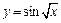 на
на 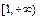 .
.
Рассмотрим разность 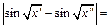
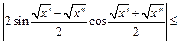
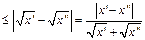 - получено с использованием неравенств:
- получено с использованием неравенств:
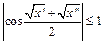 ,
, 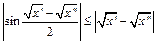 для
для 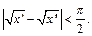
Т.к. на множестве 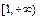 функция
функция 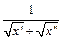 ограничена для
ограничена для 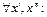
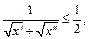 то
то 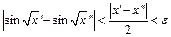 , откуда
, откуда 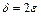 и, следовательно, функция
и, следовательно, функция 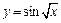 равномерно непрерывна на
равномерно непрерывна на 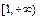 .
.
Пример 6. Исследовать на равномерную непрерывность функцию 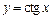 на (0, 1).
на (0, 1).
Рассмотрим разность 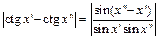 . При
. При 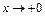 функция
функция 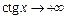 , поэтому функция
, поэтому функция 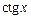 не будет равномерно непрерывной в любом интервале
не будет равномерно непрерывной в любом интервале 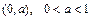 . Докажем это. Положим
. Докажем это. Положим 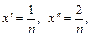 тогда
тогда 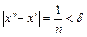 , для всех
, для всех 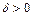 , но при этом:
, но при этом: 
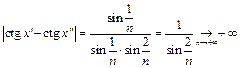 . Следовательно,
. Следовательно, 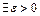 , например
, например 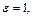
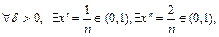
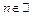 и
и 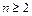 , что
, что 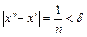 , но
, но 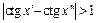 .
.
Пример 7. Исследовать на равномерную непрерывность функцию 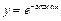 на
на 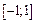 .
.
Функция определена и непрерывна как композиция непрерывных функций на замкнутом ограниченном множестве 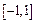 , следовательно, она является равномерно непрерывной на
, следовательно, она является равномерно непрерывной на 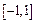 по теореме Кантора.
по теореме Кантора.
Пример 8. Исследовать на равномерную непрерывность функцию 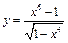 на
на 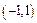 .
.
Функция не определена в точках 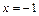 и
и 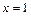 , однако существует
, однако существует 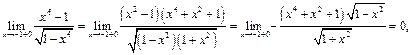 аналогично,
аналогично,
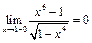 , поэтому, доопределив функцию по непрерывности в точках
, поэтому, доопределив функцию по непрерывности в точках 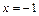 и
и 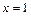 :
: 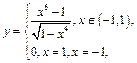
мы получим функцию, непрерывную на замкнутом ограниченном множестве 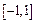 , а поэтому и равномерно непрерывную по теореме Кантора.
, а поэтому и равномерно непрерывную по теореме Кантора.
Пример 9. Исследовать на равномерную непрерывность функцию 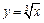 на
на 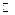 .
.
Функция 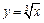 непрерывна на
непрерывна на 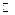 , следовательно, непрерывна и на промежутке
, следовательно, непрерывна и на промежутке 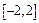 .
.
Тогда по теореме Кантора она равномерно непрерывна на 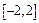 . Докажем, что данная функция равномерно непрерывна для
. Докажем, что данная функция равномерно непрерывна для 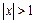 .
.
Пусть 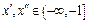 либо
либо 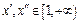 , тогда
, тогда 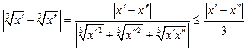 . Для
. Для 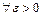 выберем
выберем 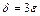 , тогда для
, тогда для 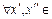
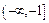 либо
либо 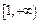 из неравенства
из неравенства 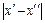
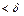 будет следовать
будет следовать 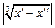
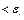 . Значит функция
. Значит функция 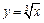 равномерно непрерывна на
равномерно непрерывна на 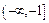 и
и 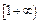 .
.  Покажем, что она равномерно непрерывна на
Покажем, что она равномерно непрерывна на 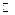 .
.
Зададимся произвольным 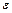 >0. В силу равномерной непрерывности на
>0. В силу равномерной непрерывности на 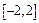
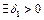 такое, что для
такое, что для 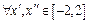 и таких, что
и таких, что 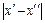 <
< 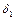 , тотчас выполняется
, тотчас выполняется 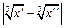 <
< 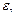 а вследствие равномерной непрерывности на
а вследствие равномерной непрерывности на 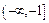 либо
либо 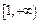
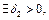 что для
что для 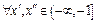 либо
либо 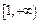 , для которых
, для которых 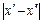 <
< 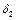 , имеет место:
, имеет место: 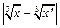 <
< 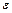 . Возьмем
. Возьмем 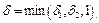 Тогда для
Тогда для 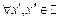 из неравенства
из неравенства 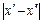 <
< 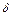 будет, во-первых, следовать (т.к.
будет, во-первых, следовать (т.к. 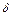 <1), что
<1), что 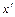 и
и 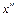 оба принадлежат либо
оба принадлежат либо 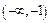 , либо
, либо 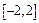 , либо
, либо 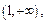 а во-вторых, что
а во-вторых, что 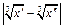 <
< 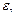 что и означает равномерную непрерывность
что и означает равномерную непрерывность 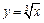 на
на 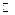 .
.
Пример 10.Доказать, что если функция 
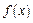 определена и непрерывна при
определена и непрерывна при 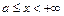 и существует конечный
и существует конечный 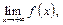 то
то 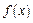 равномерно непрерывна на данном промежутке.
равномерно непрерывна на данном промежутке.
Из существования предела согласно критерию Коши имеем, что для 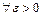
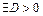 такое, что для
такое, что для 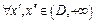 (т.е. для
(т.е. для 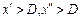 )
)  тотчас выполняется:
тотчас выполняется: 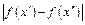 <
< 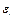 Фиксируем найденное D и рассмотрим сегмент
Фиксируем найденное D и рассмотрим сегмент 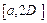 . Согласно теореме Кантора функция
. Согласно теореме Кантора функция 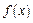 равномерно непрерывна на
равномерно непрерывна на 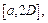 т.е. для
т.е. для 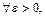 в том числе и для
в том числе и для 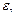 выбранного ранее,
выбранного ранее, 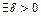 такое, что для
такое, что для 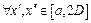 и таких, что
и таких, что 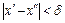 выполняется
выполняется 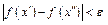
Не ограничивая общности, считаем, что 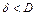 . Тогда из условия
. Тогда из условия 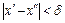 следует, что числа
следует, что числа 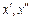 либо оба больше D, либо оба меньше 2D (т.е. не может быть, чтобы
либо оба больше D, либо оба меньше 2D (т.е. не может быть, чтобы 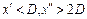 ). Но в обоих этих случаях из условия
). Но в обоих этих случаях из условия 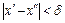 сразу следует:
сразу следует: 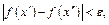 что и устанавливает равномерную непрерывность на
что и устанавливает равномерную непрерывность на 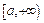 функции
функции 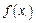 .
.
Пример 11.Исследовать на равномерную непрерывность функцию 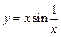 на
на 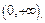
Функция 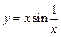 не определена в точке
не определена в точке 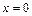 , однако может быть доопределена по непрерывности, т.к.
, однако может быть доопределена по непрерывности, т.к. 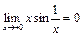 как произведение ограниченной функции на бесконечно малую. Поэтому положим
как произведение ограниченной функции на бесконечно малую. Поэтому положим 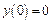 . Найдем
. Найдем 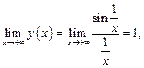 откуда по доказанному в примере 10 следует равномерная непрерывность функции
откуда по доказанному в примере 10 следует равномерная непрерывность функции 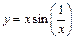 на
на 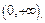
 2015-02-14
2015-02-14 2209
2209








