Пусть функция 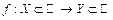 определена в окрестности точки
определена в окрестности точки  , кроме, может быть, самой точки
, кроме, может быть, самой точки  . Точку
. Точку  называют точкой разрыва функции
называют точкой разрыва функции 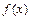 в следующих случаях:
в следующих случаях:
а) функция 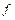 не определена в этой точке;
не определена в этой точке;
б) функция 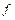 определена в точке
определена в точке  , но либо не существует
, но либо не существует 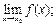 либо существует
либо существует 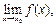 но
но 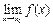 ¹
¹ 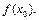
Если существует 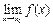 , но
, но 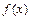 не определена в точке
не определена в точке  или
или 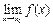 ¹
¹ 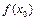 , то
, то  называют точкой устранимого разрыва.
называют точкой устранимого разрыва.
Если в точке  существуют конечные пределы
существуют конечные пределы 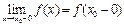
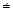
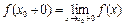 , то
, то  называют точкой разрыва 1-го рода или скачком, величину скачка характеризует модуль разности
называют точкой разрыва 1-го рода или скачком, величину скачка характеризует модуль разности 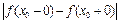 .
.
Если в точке  не существует хотя бы один из пределов
не существует хотя бы один из пределов 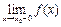 или
или 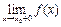 , то
, то  называют точкой разрыва второго рода.
называют точкой разрыва второго рода.
Функция, имеющая хотя бы одну точку разрыва, называется разрывной.
Пример 1. На языке ²e-δ² доказать непрерывность следующих функций: а) 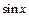 , б)
, б) 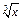 ; в)
; в) 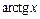 ;
;
а) "e>0 и " 
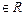 имеем:
имеем: 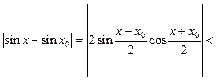
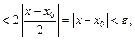 в случае
в случае 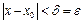 .
.

 Отметим:
Отметим: 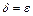 не зависит от рассматриваемой точки
не зависит от рассматриваемой точки 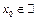 .
.
б) Пусть 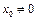 - произвольная точка из
- произвольная точка из 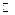 . Тогда
. Тогда 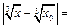
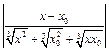 =
= 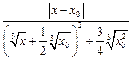
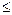
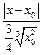
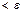 , если
, если 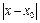 <
< 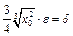 . Итак,
. Итак, 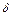 зависит и от
зависит и от 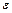 , и от значения
, и от значения  . В точке
. В точке  = 0 непрерывность функции следует из неравенства:
= 0 непрерывность функции следует из неравенства: 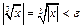 , справедливого при
, справедливого при 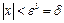 .
.
|
|
|
в) Пусть 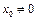 .
.
При доказательстве воспользуемся неравенством 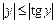 при
при 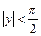 и формулой
и формулой 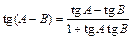 . Получим:
. Получим: 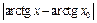
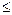
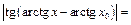
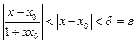 , ведь можно считать, не нарушая общности рассуждений, что
, ведь можно считать, не нарушая общности рассуждений, что 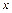 и
и  одного знака, т.е.
одного знака, т.е. 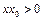 . Здесь
. Здесь 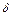 зависит только от
зависит только от 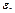
Непрерывность функции 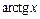 в точке
в точке 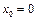 следует из неравенства
следует из неравенства 
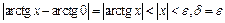 .
.
Пример 2. Сформулировать на языке “ 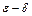 ” в положительном смысле следующее утверждение: функция
” в положительном смысле следующее утверждение: функция 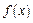 ,определенная в точке
,определенная в точке  , не является непрерывной в этой точке.
, не является непрерывной в этой точке.
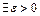
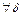
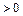 ,
, 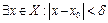 , но
, но 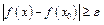 .
.
Пример 3. Пусть для 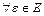 можно найти соответствующие числа
можно найти соответствующие числа 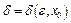
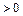 такие, что
такие, что 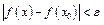 , если только
, если только 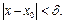
Можно ли утверждать, что функция 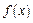 непрерывна в точке
непрерывна в точке  , если:
, если:
а) 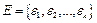 ; б)
; б) 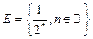 .
. 
а) функция 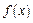 не является непрерывной в точке
не является непрерывной в точке  , так как конечное множество чисел
, так как конечное множество чисел 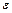 имеет
имеет 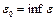 , поэтому
, поэтому 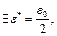 для которого согласно условию задачи
для которого согласно условию задачи 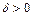 уже нельзя указать.
уже нельзя указать.
б) функция 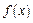 является непрерывной в точке
является непрерывной в точке  , ибо для
, ибо для 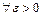
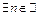 такое, что
такое, что 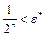
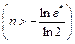 , а тогда
, а тогда 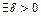 такое, что для
такое, что для 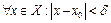 выполняется:
выполняется: 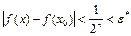 , что и означает непрерывность в точке
, что и означает непрерывность в точке  .
.
Пример 4.Найти и классифицировать точки разрыва следующих функций:
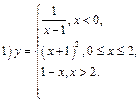
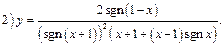

1) Функция 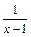 непрерывна для
непрерывна для 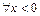 , функция
, функция 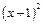 непрерывна для
непрерывна для 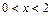 , функция
, функция 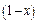 непрерывна при x>2. Рассмотрим точки
непрерывна при x>2. Рассмотрим точки 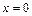 и
и 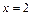 .
.
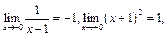 следовательно, в точке
следовательно, в точке 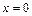 имеет место разрыв 1 рода с величиной скачка, равной 2. В точке
имеет место разрыв 1 рода с величиной скачка, равной 2. В точке 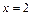
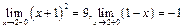 и в этой точке функция имеет разрыв 1 рода с величиной скачка, равной 10.
и в этой точке функция имеет разрыв 1 рода с величиной скачка, равной 10.
2) Из определения функции 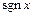 следует, что:
следует, что:
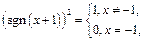
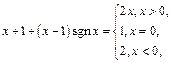
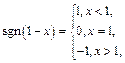
поэтому для рассматриваемой функции получим:
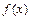 =
= 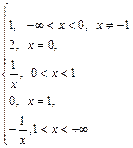
Таким образом, функция 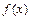 определена для всех
определена для всех 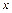 , кроме
, кроме 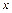 = -1. Однако,
= -1. Однако, 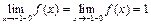 , следовательно, в точке
, следовательно, в точке 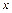 = -1 функция имеет устранимый разрыв.
= -1 функция имеет устранимый разрыв.
В точке 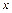 = 0 имеем:
= 0 имеем:
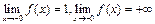 —
— 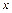 = 0 - точка разрыва второго рода.
= 0 - точка разрыва второго рода.
В точке 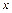 = 1
= 1 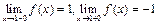 и в этой точке
и в этой точке 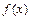 имеет разрыв 1 рода с величиной скачка, равной 2.
имеет разрыв 1 рода с величиной скачка, равной 2.
Пример 5. Установить, существует ли значение 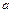 , при котором функция
, при котором функция 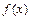 непрерывна в точке
непрерывна в точке  , если
, если
|
|
|
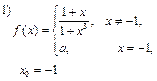
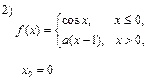
1) 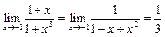 , поэтому функция будет непрерывна в точке
, поэтому функция будет непрерывна в точке 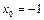 , если
, если 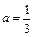 .
.
2) Так как 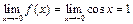 , то
, то 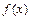 будет непрерывной в точке
будет непрерывной в точке 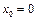 , если
, если 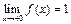 , т.е.
, т.е. 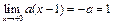 , откуда
, откуда 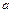 = -1.
= -1.
Пример 6.Установить, существуют или не существуют значения 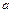 и
и 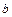 , при которых
, при которых 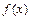 непрерывна в своей области определения, если:
непрерывна в своей области определения, если:
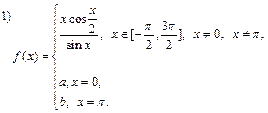
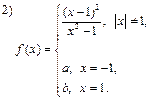
1) Найдем 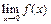 и
и 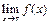 :
:
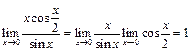 , поэтому
, поэтому 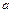 = 1;
= 1;
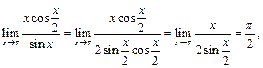 поэтому
поэтому 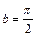 . При
. При 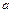 = 1 и
= 1 и 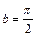 функция непрерывна на
функция непрерывна на 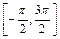 .
.
2) Хотя существует 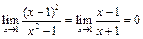 , но
, но 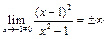 , поэтому при
, поэтому при 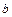 = 0 функция
= 0 функция 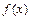 будет непрерывной в точке
будет непрерывной в точке 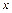 = 1, однако
= 1, однако 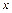 = ‑ 1 является точкой бесконечного разрыва (разрыва 2 рода) функции
= ‑ 1 является точкой бесконечного разрыва (разрыва 2 рода) функции 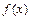 .
.
Пример 7. Исследовать на непрерывность следующие функции:
1) 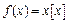 ; 2)
; 2) 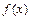
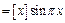 ; 3)
; 3) 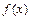 =
= 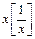 .
.
1) Учитывая, что 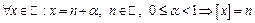 , получим, что на интервале
, получим, что на интервале 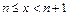 функция
функция 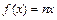 – непрерывна при
– непрерывна при 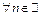 . При
. При 
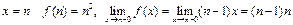 , т.е.
, т.е. 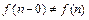 и функция
и функция 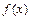 имеет разрыв 1 рода с величиной скачка, равной
имеет разрыв 1 рода с величиной скачка, равной 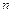 , в любой точке
, в любой точке 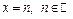 .
.
2) Для 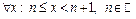
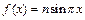 - непрерывна на указанных интервалах. Остается исследовать функцию на непрерывность в точках
- непрерывна на указанных интервалах. Остается исследовать функцию на непрерывность в точках 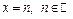 .
.
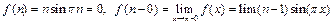 =
= 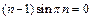 ,
, 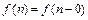 -функция
-функция 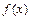 непрерывна в любой точке
непрерывна в любой точке 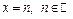 , а следовательно, непрерывна на
, а следовательно, непрерывна на 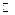 .
.
3) Область определения функции 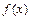 =
= 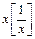 -
- 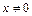 . При
. При 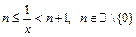 , т.е. при
, т.е. при 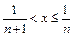 функция
функция 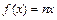 непрерывна, при этом
непрерывна, при этом 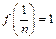 . Найдем
. Найдем 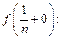
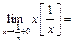
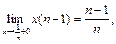 т.е.
т.е. 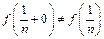 - точки
- точки 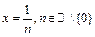 являются точками разрыва 1 рода.
являются точками разрыва 1 рода.
Осталось исследовать точку 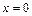 . Пусть сначала
. Пусть сначала 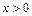 . Если
. Если 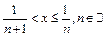 , то
, то 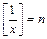 и
и 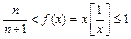 . При
. При 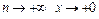 и по принципу двустороннего ограничения имеем:
и по принципу двустороннего ограничения имеем: 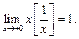 Если же
Если же 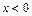 , т.е.
, т.е. 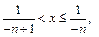
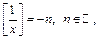 и
и 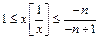 . При
. При 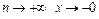 и
и 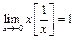 в силу принципа двустороннего ограничения. Следовательно, функция
в силу принципа двустороннего ограничения. Следовательно, функция 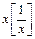 имеет в точке
имеет в точке 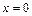 устранимый разрыв.
устранимый разрыв.
Пример 8. Обязательно ли будет разрывна в точке  сумма двух функций
сумма двух функций 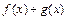 , если:
, если:
а) функция 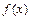 - непрерывна, а функция
- непрерывна, а функция 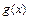 разрывна при
разрывна при 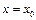 ;
;
б) обе функции 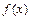 и
и 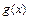 разрывны при
разрывны при 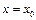 ? Построить соответствующие примеры.
? Построить соответствующие примеры.
а) Да, ведь если не существует 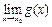 , то какова бы ни была непрерывная в точке
, то какова бы ни была непрерывная в точке  функция
функция 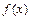 ,
, 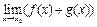 не существует.
не существует.
Например: 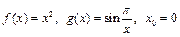 .
.
Если же 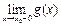 ≠
≠ 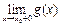 или
или 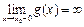 , то и
, то и 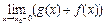 ≠
≠ 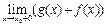 или
или 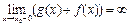 .
.
б) Нет, например: 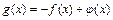 , где
, где 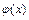 непрерывна в точке
непрерывна в точке  , тогда
, тогда 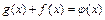 - сумма разрывных в точке
- сумма разрывных в точке  функций является непрерывной.
функций является непрерывной.
Пример 9. Обязательно ли произведение двух функций 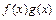 терпит разрыв непрерывности в данной точке
терпит разрыв непрерывности в данной точке  , если: а) функция
, если: а) функция 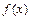 непрерывна, а функция
непрерывна, а функция 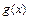 разрывна при
разрывна при 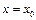 ; б) обе функции разрывны в этой точке? Построить соответствующие примеры.
; б) обе функции разрывны в этой точке? Построить соответствующие примеры.
а) Нет, например, 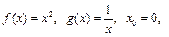 произведение
произведение 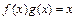 - непрерывно при
- непрерывно при 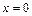 .
.
б) Нет, например:
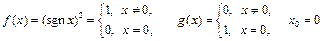 .
.
Произведение 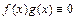 на
на 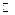 – непрерывная в точке
– непрерывная в точке 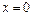 функция.
функция.
Пример 10. Можно ли утверждать, что квадрат разрывной функции тоже разрывная функция? Построить пример всюду разрывной функции, квадрат которой есть функция непрерывная.
Нет, примером функции, разрывной в любой точке, квадрат которой, тем не менее, представляет собой непрерывную функцию, является:
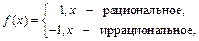 тогда
тогда 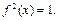
 2015-02-14
2015-02-14 3611
3611








