2015-02-04
1659
Осуществим подстановку в W(z)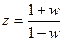 
, 
,
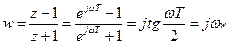где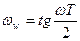 
- относительная безразмерная псевдочастота.
Введем понятие абсолютной псевдочастоты:
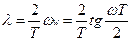, с-1; 
;
.
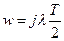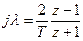При малых углах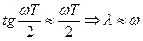 
, тогда при выполнении условия 
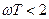можно в расчетах заменить псевдочастоту действительной круговой частотой, что может быть использовано, в частности, при расчетах реакции ЦАС на медленно меняющиеся гармонические сигналы на входе.
Получим псевдочастотную передаточную функцию разомкнутой цифровой системы
/ 
= 
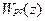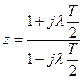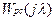, здесь 
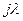соответствует р непрерывной системы, поэтому ЛПЧХ строятся по правилам для непрерывных систем. Затем применяется критерий устойчивости Найквиста для ЛЧХ.
Пример 1. Пусть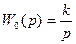 
- интегратор; 
, 
.
| |||
| |||
.
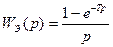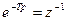Тогда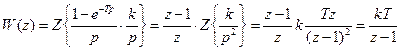 
.
Чтобы перейти к логарифмическим частотным характеристикам произведем подстановку: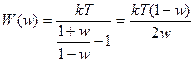 
, если вместо w подставить 
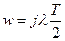, получим псевдочастотную функцию: 
.
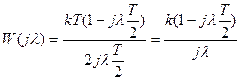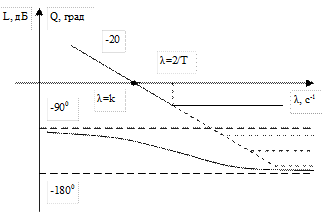
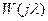- комплексный передаточный коэффициент интегрирующего звена с фиксатором 0-го порядка.
Свойства:
1. C уменьшением периода дискретизации (T®0, l=2/T ®¥) характеристика приближается к характеристике непрерывной системы;
2. Предельный фазовый сдвиг равен -p, такая замкнутая система приближается к границе устойчивости при больших k.
