Приме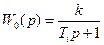р 2

Пусть , тогда

,

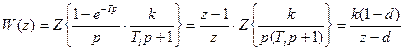где .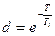

.

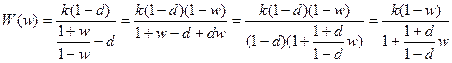Перейдем к псевдочастотным функциям:

,

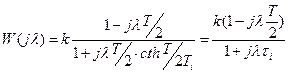так как 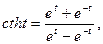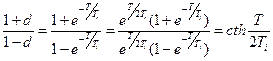. (1)

Исследуем это выражение:

1. Пусть период дискретности 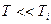[ 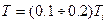] и определим :

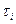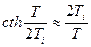, это видно из выражения (1), отсюда 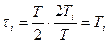, при этих соотношениях .

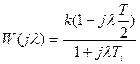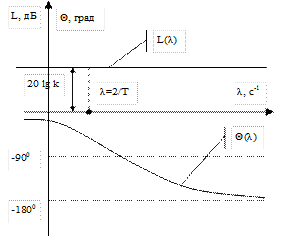
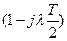- неминимально - фазовый множитель.

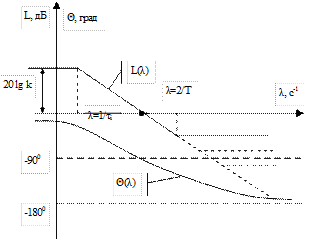
2. Пусть , тогда , .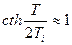

.

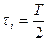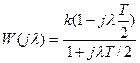Построим частотные характеристики:

1. 2.

Пример 3.

Построить логарифмические псевдочастотные характеристики системы, если передаточная функция непрерывной части имеет вид

.

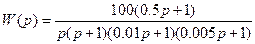Экстраполятор нулевого порядка.

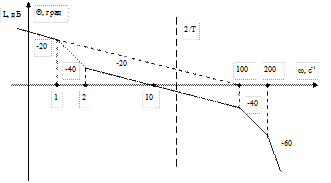
Зададим период дискретности T=0.1с. На графике отложим частоту 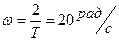, выделим НЧ и ВЧ части характеристики;

, .

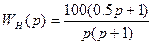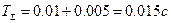Теперь запишем выражение для псевдочастотной функции:

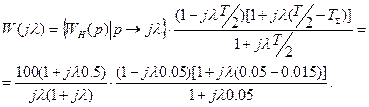
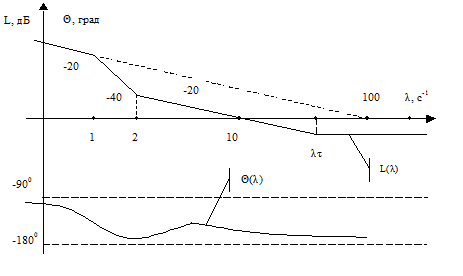
На основании этого выражения построим ЛПЧХ, где .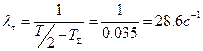

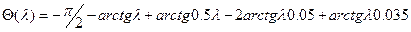Замечание: фазовые характеристики непрерывных и цифровых систем существенно различаются.