 Пусть известен многочлен знаменателя дискретной передаточной функции цифровой САУ
Пусть известен многочлен знаменателя дискретной передаточной функции цифровой САУ 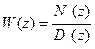 , где
, где 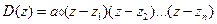 ,
, 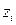 - корни характеристического уравнения системы.
- корни характеристического уравнения системы.
Если корень характеристического уравнения располагается внутри круга единичного радиуса, то при изменении 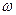 от
от 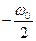 до
до 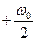
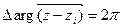 . Если вне круга, то
. Если вне круга, то 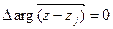 ,
, 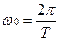 , T – период квантования сигналов.
, T – период квантования сигналов.
Будем рассматривать 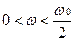 .
.
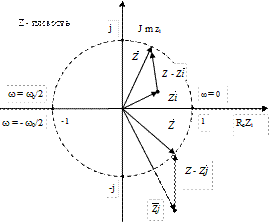
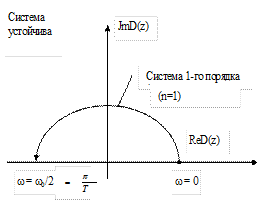
Формулировка критерия Михайлова:
«Для того чтобы система была устойчива, необходимо и достаточно, чтобы при изменении ω от 0 до 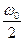 характеристический вектор
характеристический вектор 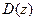 имел приращение аргумента
имел приращение аргумента 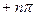 , где n – степень характеристического уравнения системы».
, где n – степень характеристического уравнения системы».
Кривая Михайлова должна поворачиваться на угол np.
Если имеются полюсы на окружности единичного радиуса (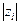 =1), а все остальные – внутри круга, то цифровая система находится на границе устойчивости. Если это полюс
=1), а все остальные – внутри круга, то цифровая система находится на границе устойчивости. Если это полюс 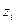 =+1, то цифровая система называется нейтральной.
=+1, то цифровая система называется нейтральной.
Цифровые системы первого и второго порядка, в отличие от непрерывных систем такого же порядка, могут быть неустойчивыми даже при положительных коэффициентах характеристического уравнения. Это объясняется тем, что фиксатор, содержащийся обычно в контуре цифровой системы, вносит дополнительное отставание по фазе.
Пример.

|
|
 2015-02-04
2015-02-04 516
516

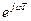 )-кривая Михайлова
)-кривая Михайлова







