Формулировка критерия Гурвица для непрерывных систем справедлива и для дискретных систем, если в характеристическом уравнении системы произвести замену 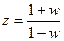 .
.
Введем комплексную переменную w, связанную с комплексной переменной z билинейным преобразованием:
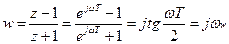 , где
, где 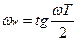 , относительная безразмерная
, относительная безразмерная
псевдочастота.
Тогда, произведя замену в характеристическом полиноме 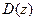 |
| 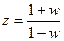 , получим характеристический полином
, получим характеристический полином 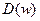 , по которому определим устойчивость системы по критерию Гурвица.
, по которому определим устойчивость системы по критерию Гурвица.
При изменении частоты 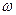 в пределах
в пределах 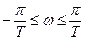 относительная псевдочастота
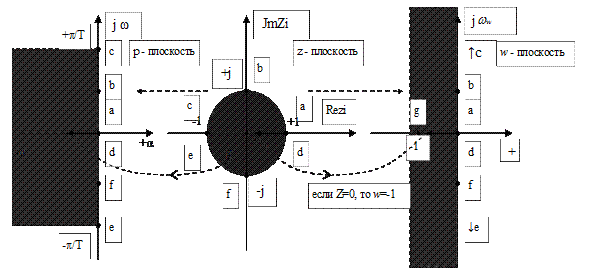
относительная псевдочастота  пробегает все значения от -¥ до +¥, а комплексная переменная w движется по оси мнимых чисел от -j¥ до +j¥. Внутренняя часть круга единичного радиуса отображается при этом на левую полуплоскость.
пробегает все значения от -¥ до +¥, а комплексная переменная w движется по оси мнимых чисел от -j¥ до +j¥. Внутренняя часть круга единичного радиуса отображается при этом на левую полуплоскость.
При помощи w - преобразования осуществляется конформное отображение внутренности окружности единичного радиуса на плоскости z в левую полуплоскость w. При этом контур окружности единичного радиуса переходит в мнимую ось плоскости w.
При исследовании дискретных систем по преобразованным при помощи w - преобразования передаточным функциям могут использоваться обычные приемы и критерии, справедливые для непрерывных систем, в том числе и критерий Гурвица.
|
|
|
 2015-02-04
2015-02-04 587
587








