Пусть в пространстве задана ось 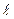 , т. е. направленная прямая.
, т. е. направленная прямая.
Проекцией точки М на ось 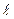 называется основание М
называется основание М  перпендикуляра ММ
перпендикуляра ММ  , опущенного из точки на ось.
, опущенного из точки на ось.
Если точка М и ось 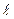 находятся в трехмерном пространстве, то точка М
находятся в трехмерном пространстве, то точка М 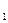 есть точка пересечения оси
есть точка пересечения оси 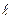 с плоскостью, проходящей через точку М перпендикулярно оси
с плоскостью, проходящей через точку М перпендикулярно оси 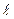 .
.
Если точка М лежит на оси 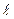 , то проекция точки М на ось совпадает с самой точкой М.
, то проекция точки М на ось совпадает с самой точкой М.
Пусть 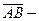 произвольный вектор (
произвольный вектор (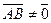 ). Обозначим через
). Обозначим через 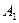 и
и 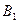 проекции на ось l соответственно начала А и конца В вектора
проекции на ось l соответственно начала А и конца В вектора 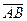 . Обозначим соответствующие проекции:
. Обозначим соответствующие проекции: 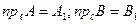
Проекцией вектора на ось называется число:
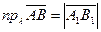 , если
, если 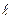 и
и 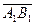 сонаправлены,
сонаправлены,
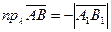 , если
, если 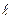 и
и 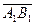 противоположно направлены,
противоположно направлены,
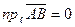 , если
, если 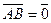 , или
, или 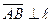 .
.
Свойства проекций:
Проекция вектора 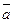 на ось
на ось 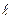 равна произведению модуля вектора на косинус угла, составленного вектором с осью
равна произведению модуля вектора на косинус угла, составленного вектором с осью 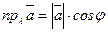
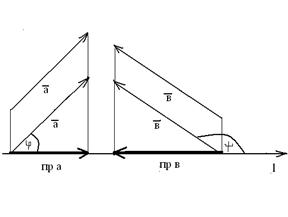 На рисунке
На рисунке 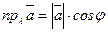 положительна, т.к.0<
положительна, т.к.0< 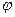 <
< 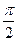 .
.
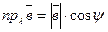 отрицательна, т.к.
отрицательна, т.к. 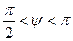 .
.
1. Проекции равных векторов на одну и ту же ось равны между собой.
2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось. 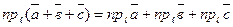
3. При умножении вектора на число, его проекция также умножается на это число. 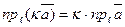
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
Линейные операции над векторами, заданными в координатной форме:
Пусть заданы два вектора: 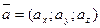 и
и 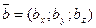 , тогда:
, тогда:
1. 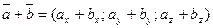
2. 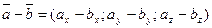
3. 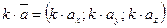
Условие коллинеарности векторов: 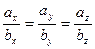 - т.е. проекции коллинеарных векторов пропорциональны.
- т.е. проекции коллинеарных векторов пропорциональны.
Док-во:Так как условие параллельности векторов 
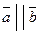 можно записать в виде:
можно записать в виде: 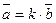 , откуда
, откуда 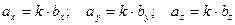 , таким образом, условие коллинеарности в координатном виде:
, таким образом, условие коллинеарности в координатном виде: 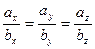
 2015-02-18
2015-02-18 494
494








