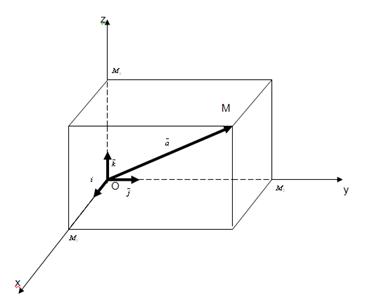
Рассмотрим в трехмерном пространстве декартову систему координат. Через начало координат - точку О проведены координатные оси: ОХ, ОУ, OZ. На осях координат выберем единичные векторы(орты),обозначаемые соответственно: 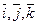 . Возьмем произвольный вектор пространства
. Возьмем произвольный вектор пространства 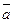 и совместим его начало с началом координат
и совместим его начало с началом координат 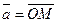 . Найдем проекции вектора
. Найдем проекции вектора 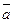 на координатные оси. Для этого через конец вектора
на координатные оси. Для этого через конец вектора 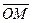 , точку М проведем плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно
, точку М проведем плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно 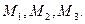 Получили прямоугольный параллелепипед, одна из диагоналей которого является вектор
Получили прямоугольный параллелепипед, одна из диагоналей которого является вектор 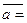
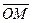 , а ребра, выходящие из вершины О являются проекциями вектора на координатные оси. Обозначим проекции вектора
, а ребра, выходящие из вершины О являются проекциями вектора на координатные оси. Обозначим проекции вектора 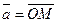 на оси ОХ, ОУ, OZ соответственно через
на оси ОХ, ОУ, OZ соответственно через 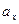 ;
; 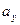 ;
; 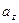 .
.
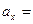
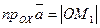 =
= 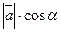 , где
, где 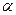 -угол между вектором
-угол между вектором 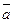 и осью ОХ.
и осью ОХ.
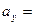
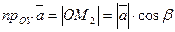 , где
, где 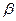 - угол между вектором
- угол между вектором 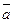 и осью ОУ.
и осью ОУ.
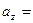
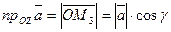 , где
, где 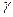 -угол между вектором
-угол между вектором 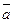 и осью OZ.
и осью OZ.
Так как 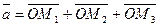 =
= 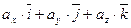 . Полученное векторное равенство часто записывается в символьном виде:
. Полученное векторное равенство часто записывается в символьном виде: 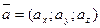 .
.
Получается формула разложения вектора по ортам координатных осей:
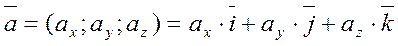 |
Проекции вектора на соответствующие оси называются координатами вектора 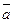 , соответственно:
, соответственно: 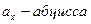 ,
, 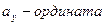 ,
, 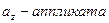 . Два вектора равны, если равны их координаты. Зная координаты вектора, можно вычислить его модуль.
. Два вектора равны, если равны их координаты. Зная координаты вектора, можно вычислить его модуль.
Модуль вектора равен корню квадратному из суммы квадратов его координат.
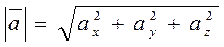 |
Нормировать вектор, значит, сделать его единичной длины, можно, разделив вектор на модуль вектора: 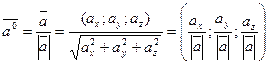
 2015-02-18
2015-02-18 1421
1421
