Векторы

Величины, которые полностью определяются своим численным значением, называются скалярными. Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными.

Вектор -это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А- начало вектора, а В- его конец, то вектор обозначается символом 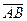, или 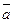. Вектор 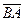(у него начало в точке В, а конец в точке А) называется противоположным вектору 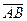. Вектор, противоположный вектору 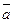, обозначается .

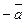Длиной или модулем вектора 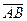называется длина отрезка AB и обозначается 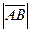. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 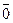. Нулевой вектор направления не имеет. Вектор единичной длины, направление которого совпадает с направлением вектора 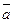, называется ортом вектора 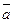и обозначается .

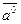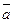
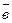Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначаются коллинеарные векторы ║

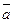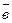
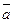
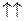
Коллинеарные векторы могут быть направлены одинаково, т.е. быть сонаправленными ( 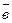), или быть противоположно направленными ().

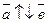Нулевой вектор считается коллинеарным любому вектору.

Два вектора 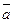и 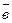называются равными (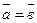), если они коллинеарные, одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора перемешать в любую точку пространства.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или хотя бы два коллинеарные, то такие векторы будут компланарны.