2015-02-18
295
Произведением вектора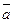 
на скаляр (число) 
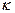называется вектор 
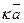, который удовлетворяет следующим условиям:
· 
· 
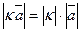
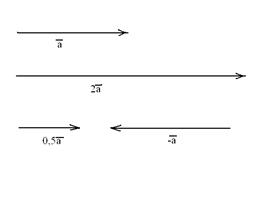
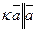, т.е. векторы 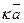и 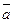коллинеарны
· 
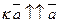, е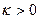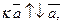сли 
, 
если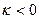 
Линейные операции над векторами обладают следующими свойствами:
1. 
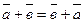
2. 
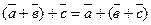
3. 
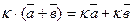
4. 
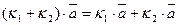
Эти свойства позволяют производить преобразования в линейных операциях с векторами так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
