Пусть заданы два вектора 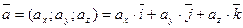 и
и 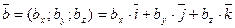 . Составим таблицу скалярных произведений орт:
. Составим таблицу скалярных произведений орт:
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения орт 
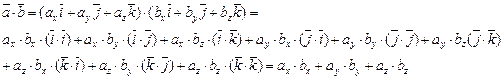

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
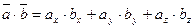 |
Пример 1. Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-3;2;2), С(2;5;1), D(3;-2;2), взаимно перпендикулярны.
Решение: Составим вектора 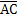 и
и 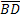 , лежащие на диагоналях данного четырехугольника. Имеем:
, лежащие на диагоналях данного четырехугольника. Имеем: 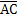 =(6;9;-3) и
=(6;9;-3) и 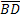 =(6;-4;0). Найдем скалярное произведение этих векторов:
=(6;-4;0). Найдем скалярное произведение этих векторов: 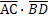 =36-36-0=0.
=36-36-0=0.
Отсюда следует, что 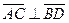 . Т.е. диагонали четырехугольника ABCD взаимно перпендикулярны.
. Т.е. диагонали четырехугольника ABCD взаимно перпендикулярны.
Некоторые приложения скалярного произведения
Определение косинуса угла 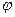 между двумя ненулевыми векторами:
между двумя ненулевыми векторами:
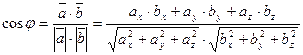 |
Отсюда следует условие перпендикулярности двух ненулевых векторов:
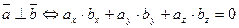
Проекция вектора на заданное направление
Нахождение проекции вектора 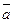 в направлении
в направлении 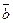 :
:
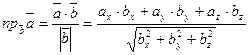 |
 2015-02-18
2015-02-18 4584
4584
