Прямая, проходящая через точку, параллельно данному вектору

Опр: Направляющим вектором прямой называется вектор, параллельный данной прямой.

Составим уравнение прямой 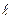, проходящей через точку 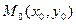, параллельно вектору .

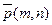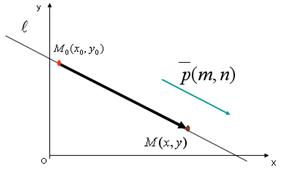Возьмем произвольную точку М(х,у), принадлежащую прямой, составим вектор 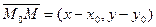. Векторы 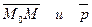должны быть коллинеарны, следовательно. Их координаты должны быть пропорциональны, т.е.

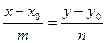
Данная форма записи уравнения прямой называется каноническое уравнение прямой. Для того, чтобы преобразовать каноническое уравнение в общий вид, необходимо разрешить пропорцию: ; ;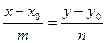

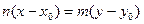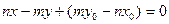
Прямую, заданную в каноническом виде можно представить в параметрическом виде, для этого введем параметр p, и каждое отношение приравняем к параметру t. Решим полученные уравнения относительно x и y:

; ;

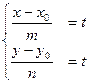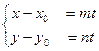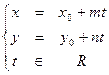
Получено параметрическое уравнение прямой линии на плоскости.