Пусть необходимо спроектировать точку 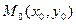 на прямую
на прямую 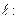 Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор
Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор 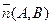 . Составим уравнение проецирующей прямой. Она проходит через точку
. Составим уравнение проецирующей прямой. Она проходит через точку 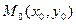 и параллельна вектору
и параллельна вектору 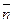 . Подставив координаты точки и вектора в каноническое уравнение прямой
. Подставив координаты точки и вектора в каноническое уравнение прямой 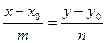 , получим:
, получим: 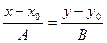 . Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему:
. Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему: 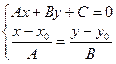 решение этой системы есть координаты точки, являющейся проекцией точки
решение этой системы есть координаты точки, являющейся проекцией точки 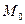 на прямую
на прямую 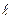
Пример: Даны вершины треугольника 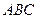 :
: 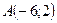 ;
; 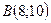 ;
; 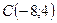 . Найти:
. Найти:
1) уравнение высоты, опущенной из вершины 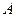 ;
;
2) точку пересечения высоты 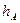 и стороны
и стороны 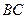 ;
;
3) точку пересечения медиан треугольника 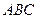 .
.
Решение: 1) Составим уравнение высоты 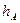 , проходящей через точку
, проходящей через точку 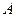 перпендикулярно вектору
перпендикулярно вектору 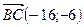 :
:
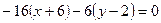 ;
; 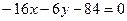 ,
, 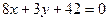 .
.
Ответ: 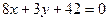 .
.
2) Составим уравнение стороны 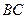 :
:
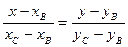 ,
, 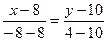 ,
, 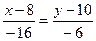 ,
,
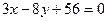 .
.
Найдем точку пересечения высоты 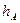 и стороны
и стороны 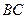 .Обозначим эту точку N, она является проекцией точки А на сторону ВС. Для нахождения точки N, решим следующую систему уравнений:
.Обозначим эту точку N, она является проекцией точки А на сторону ВС. Для нахождения точки N, решим следующую систему уравнений:
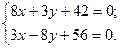
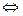
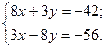
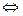
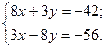
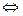
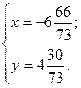
Ответ: N 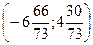 .
.
3) Найдем середину стороны 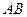 :
:
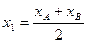 ,
, 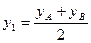 ,
, 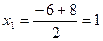 ,
, 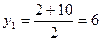 .
.
Составим уравнение прямой проходящей через точку 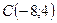 и точку М
и точку М 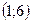 :
:
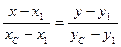 ,
, 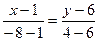 ,
, 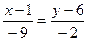 ,
,
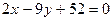 .
.
Найдем середину стороны 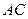 :
:
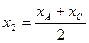 ,
, 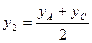 .
.
 ,
, 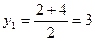 .
.
Составим уравнение прямой проходящей через точку 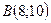 и точку N
и точку N 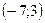 :
:
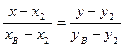 ,
, 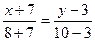 ,
, 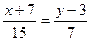 ,
,
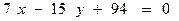 .
.
Найдем точку О пересечения найденных медиан:

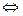
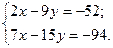
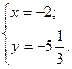
Ответ: О 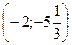 .
.
 2015-02-18
2015-02-18 5026
5026
