2015-02-18
6778
Опр.: Нормалью к плоскости называется вектор, перпендикулярный к данной плоскости.
Пусть необходимо составить уравнение плоскости, проходящей через заданную точку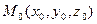 
и перпендикулярной вектору 
.
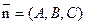Предположим, что такая плоскость построена, возьмем на ней произвольную точку М(x,y,z). Составим вектор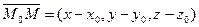 
. Вектор 
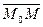перпендикулярен вектору 
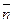, следовательно, их скалярное произведение равно нулю: 
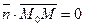, это условие имеет вид::
 |
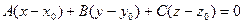Данный способ задания плоскости называется плоскость по точке М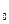 
(
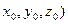и нормали 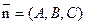. Имея уравнение плоскости в общем виде: Ax+ By+ Cz+ D=0, можно выписать нормаль к плоскости .
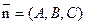Пример: Составить уравнение плоскости, проходящей через точку А(1,2,-3), параллельно плоскости 3x-4y+5z-2=0
Решение: Выпишем нормаль к плоскости, т.е. вектор перпендикулярный плоскости: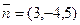 
. Так как необходимо построить плоскость параллельную данной, то можно использовать вектор 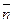в качестве нормали к искомой плоскости. Составляем уравнение плоскости по точке А и нормали : 
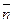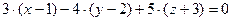после преобразования получим: 3x-4y+5z+20=0
Ответ: 3x-4y+5z+20=0.
