Пересечение прямой и плоскости

Пусть плоскость 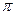задана своим общим уравнением: Ax+By+Cz+D=0, а прямая 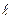в каноническом виде: 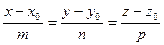. Для решения этой задачи проще всего: прямую представить в параметрическом ви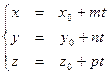де: где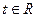

Подставляя выражения для x,y и z в уравнение плоскости: 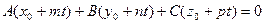, если:

· данное уравнение имеет единственное решение, то прямая и плоскость пересекаются и для нахождения точки пересечения, необходимо найденное значение параметра t подставить в параметрическое уравнение прямой

· если уравнение решения не имеет, то прямая параллельна плоскости

· если решений множество, т.е. уравнение верно при любом t, то прямая принадлежит плоскости.