Алгебраическое уравнение второго порядка на плоскости описывает кривую второго порядка, другими словами, любое уравнение вида 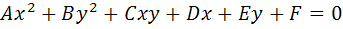 определяет либо одну из кривых: эллипс, гипербола, парабола; либо распадается на две прямые, ибо точек, удовлетворяющих данному уравнению на плоскости нет.
определяет либо одну из кривых: эллипс, гипербола, парабола; либо распадается на две прямые, ибо точек, удовлетворяющих данному уравнению на плоскости нет.
Эллипс
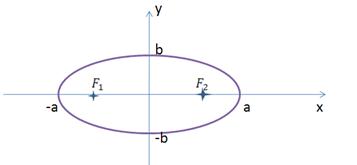 Каноническое уравнение эллипса, с центром в начале координат:
Каноническое уравнение эллипса, с центром в начале координат: 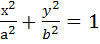
Полуосями этого эллипса являются по оси ОХ- отрезок а, и по оси ОУ- отрезок b. Таким образом, эллипс имеет две оси симметрии: ось ОХ и ось ОУ. Четыре вершины: точки с координатами (-а;0); (а;0); (0;-b); (0;b). Если величина а 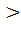 b, то
b, то 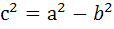 . На большей оси в точках с координатами
. На большей оси в точках с координатами 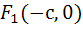 и
и 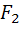 (с, 0) находятся фокусы эллипса. Эксцентриситетом эллипса называется
(с, 0) находятся фокусы эллипса. Эксцентриситетом эллипса называется 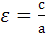 ,т.е. отношение половины расстояния между фокусами к большей полуоси. Для эллипса
,т.е. отношение половины расстояния между фокусами к большей полуоси. Для эллипса 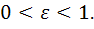
Характеристическое свойство эллипса: Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, постоянна и равна удвоенной большей полуоси.
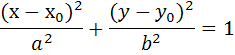
-каноническое уравнение эллипса,
центр симметрии которого находится в точке Q(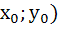 ,
,
полуоси эллипса: по ОХ равна a, по оси ОУ равна b.
Фокусы находятся в точках: 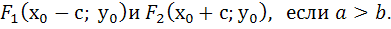
Пример: Построить эллипс, каноническое уравнение которого:
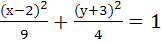 ,найти его фокусы и эксцентриситет.
,найти его фокусы и эксцентриситет.
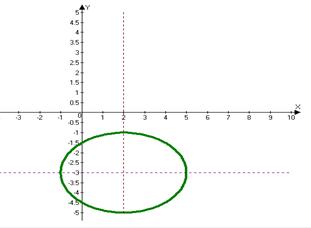
Решение: Центром симметрии эллипса является точка Q(2; -3), полуоси эллипса: а=3; b=2; 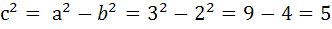 ; фокусы эллипса находятся в точках:
; фокусы эллипса находятся в точках: 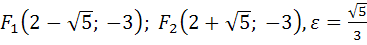 .
.
 2015-02-18
2015-02-18 734
734








