Примеры с решениями. Решение. Для того, чтобы избавиться от квадратного корня, обе части уравнения возведем в квадрат и получим

1.1 Решить уравнение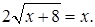

Решение. Для того, чтобы избавиться от квадратного корня, обе части уравнения возведем в квадрат и получим

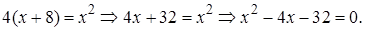
Применим формулу (1.2) и найдем 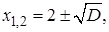где дискриминант 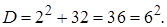Тогда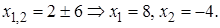

Для проверки найденные значения 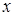подставим в исходное уравнение.

1) При 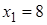получаем 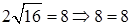– верное числовое равенство. Следовательно, 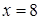– корень заданного уравнения.

2) Значение 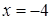корнем (решением) не является, так как получается 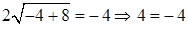– неверное числовое равенство.

Ответ: 8.

Замечание. Корни уравнения 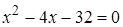можно найти, применив теорему Виета (1.3):

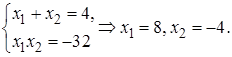
1.2 Решить уравнение 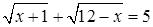и в ответе записать наибольший корень.

Решение. Приведем уравнение к виду 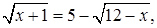после чего обе части возведем в квадрат. Получим

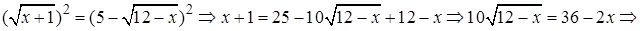
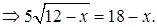Снова обе части возведем в квадрат и получим

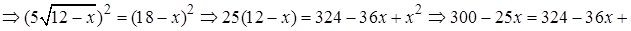
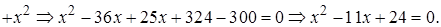Вычислим дискриминант 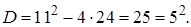Тогда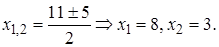

Проверка. 1) 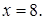Тогда

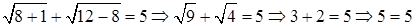(истина).

2) 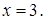Тогда

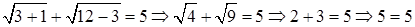(истина).

Ответ: 8.

Замечание. Если применить теорему Виета (1.3), то установим, что

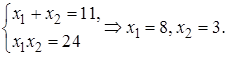
1.3 Решить уравнение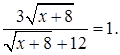

Решение.

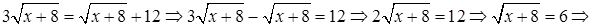
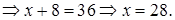
Проверка.

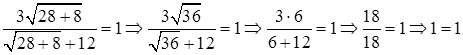(истина).

Ответ: 28.

Замечание. Можно ввести новую переменную так, что 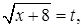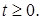Тогда исходное уравнение примет вид

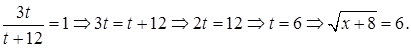
1.4 Решить уравнение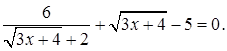

Решение. Положим 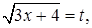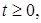и приведем заданное уравнение к виду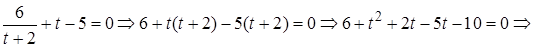

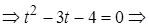
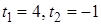не удовлетворяет условию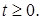

Тогда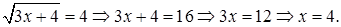

Проверка. Значение 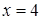подставим в исходное уравнение и получим 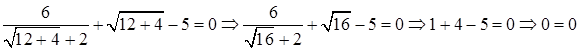(истина).

Ответ: 4.

1.5 Решить уравнение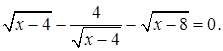

Решение. Преобразуем заданное уравнение, умножив обе его части на 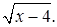Получим

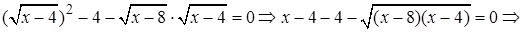
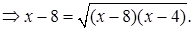Возведем обе части в квадрат:

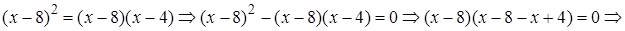
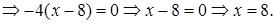
Проверка.

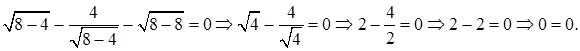
Ответ: 8.

1.6 Решить уравнение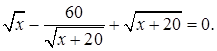

Решение. Умножим обе части уравнения на 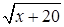и получим

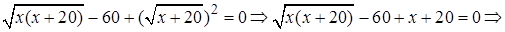
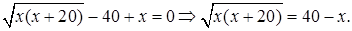
Возведение обеих частей последнего уравнения в квадрат приводит к уравнению

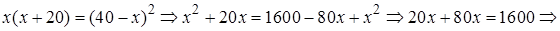
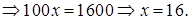
Проверка.

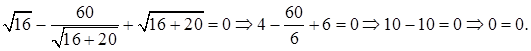
Ответ: 16.

1.7 Решить уравнение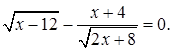

Решение. Преобразуем исходное уравнение к виду

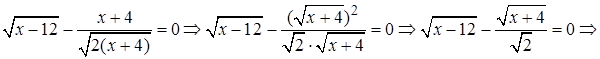
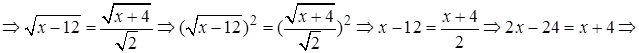
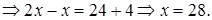
Проверка.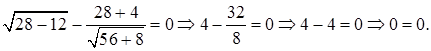

Ответ: 28.

Замечание. Можно было поступить несколько иначе:

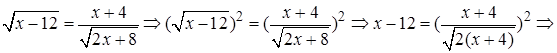
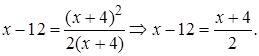
1.8 Решить уравнение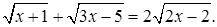

Решение.

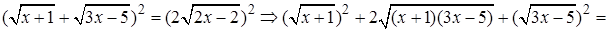
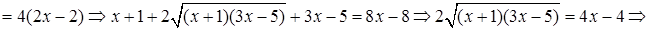
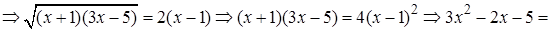
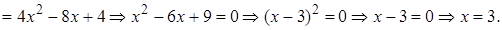
Проверка.

Ответ: 3.

1.9 Решить уравнение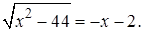

Решение.

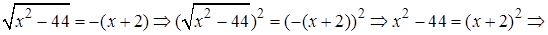
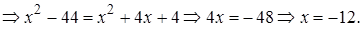
Проверка.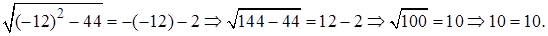

Ответ: -12.

1.10 Решить уравнение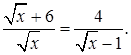

Решение. Положим 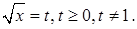Получаем уравнение

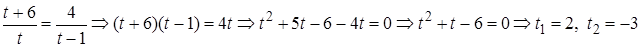не удовлетворяет условию 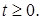Следовательно,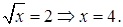

Проверка.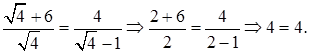

Ответ: 4.