Примеры с решениями. 2.1Найти сумму корней уравнения

2.1 Найти сумму корней уравнения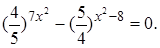

Решение. Приведем уравнение к простейшему виду и приравняем пока-

затели. Получим

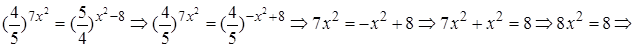
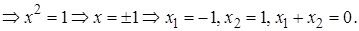
Ответ: 0.

2.2 Решить уравнение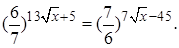

Решение. Так как 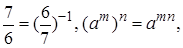то уравнение запишется в виде

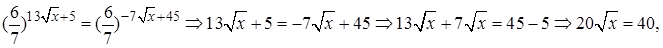
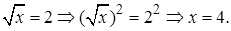
Проверка.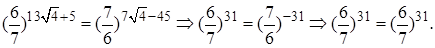

Ответ: 4.

Замечание. При решении примера 2.2 проверка обязательна, так как заданное уравнение является не только показательным, но и иррациональным.

2.3 Решить уравнение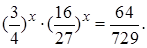

Решение. На основании правила 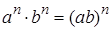получаем уравнение

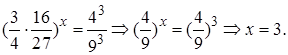
Ответ: 3.

2.4 Вычислить 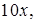где 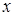– решение уравнения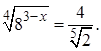

Решение. Учитывая, что

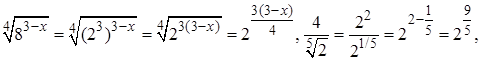
перейдем в исходном уравнении к основанию 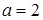и запишем его в виде

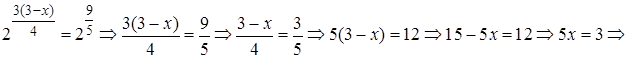
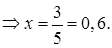Вычислим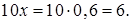

Ответ: 6.

2.5 Решить уравнение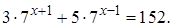

Решение. Вынесем за скобки 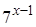(степень с меньшим показателем) и получим

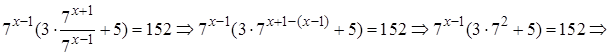
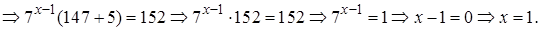
Ответ: 1.

Замечания: 1) Заданное уравнение можно решить иначе, используя свойства 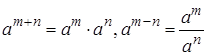степеней с одним основанием. Получаем

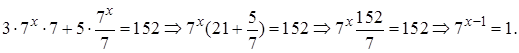
2) Приведя заданное уравнение к виду 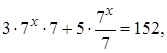можно было

ввести новую переменную, положив 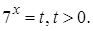Тогда уравнение преобразуется к виду

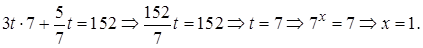
Сведение уравнения к линейному с помощью замены переменной считаем нецелесообразным.

2.6 Решить уравнение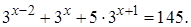

Решение. В левой части уравнения вынесем за скобки общий множитель 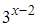и установим, что

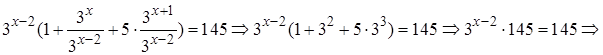
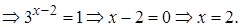
Ответ: 2.

2.7 Решить уравнение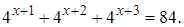

Решение.

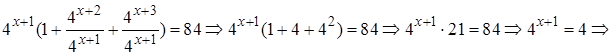
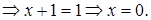
Ответ: 0.

2.8 Решить уравнение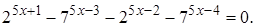

Решение. Сгруппируем члены уравнения следующим образом:

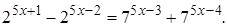
В каждой из частей вынесем общие множители и получим

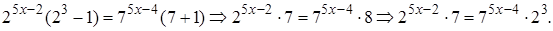
Обе части последнего уравнения разделим на его правую часть:

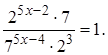
Применим правило деления степеней с одним основанием и по-

лучим

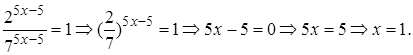
Ответ: 1.

2.9 Решить уравнение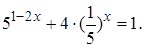

Решение. Представим уравнение в виде

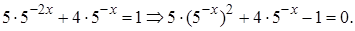
Введем замену 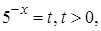и получим 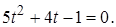Вычислим дискриминант 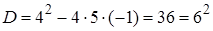и значения t. Находим 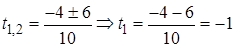не удовлетворяет условию 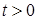, 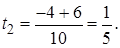Следовательно,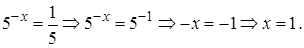

Ответ: 1.

2.10 Найти целый корень уравнения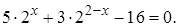

Решение. Запишем уравнение следующим образом:

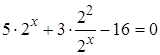
и введем величину t так, что 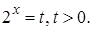Получим уравнение

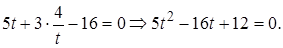
Находим 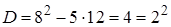и значения t:

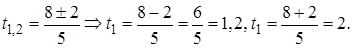
Тогда 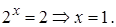Уравнение 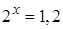целого корня не имеет.

Ответ: 1.