7.1 Объем правильной треугольной призмы равен 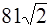 , сторона основания равна 6. Найти
, сторона основания равна 6. Найти 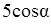 , где
, где 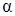 – угол между диагоналями двух боковых граней, проведенными из одной и той же вершины (рис. 7.1).
– угол между диагоналями двух боковых граней, проведенными из одной и той же вершины (рис. 7.1).
Решение. Дано: 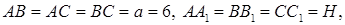
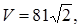
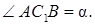 Найти
Найти 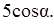
Так как
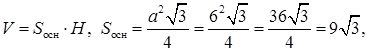
то для нахождения ребра H получаем уравнение
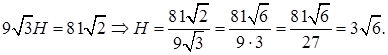
Применив теорему Пифагора, из 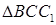 найдем диагональ
найдем диагональ 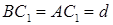 боковой грани
боковой грани
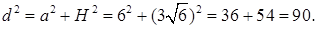
Теперь к 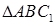 применим теорему косинусов и получим уравнения для нахождения
применим теорему косинусов и получим уравнения для нахождения 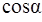 .
.
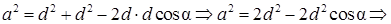
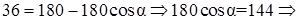
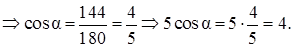
Ответ: 4.
7.2 Основанием прямой призмы является равносторонний треугольник.
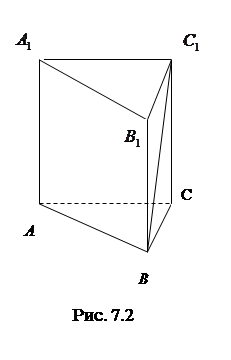 Объем призмы равен
Объем призмы равен 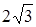 , площадь ее боковой поверхности равна 24. Вычислить
, площадь ее боковой поверхности равна 24. Вычислить 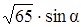 , где
, где 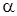 - угол наклона диагонали боковой грани к плоскости основания (рис.7.2).
- угол наклона диагонали боковой грани к плоскости основания (рис.7.2).
Решение. Дано: 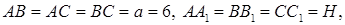
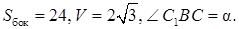 Найти
Найти 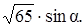
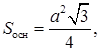 поэтому
поэтому
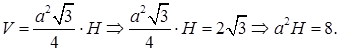
Далее,
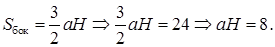
Получаем систему уравнений  и решаем ее делением первого уравнения на второе. Получаем
и решаем ее делением первого уравнения на второе. Получаем
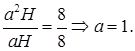
Тогда ребро (высота) призмы 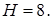
Из треугольника 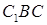 находим диагональ боковой грани
находим диагональ боковой грани
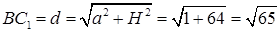 и
и 
Ответ: 8.
7.3 Основанием прямой призмы является равнобедренный треугольник. Объем призмы равен 240. Диагональ одной из равных боковых граней наклонена к плоскости основания под углом, синус которого равен 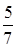 . Сумма длин этой диагонали и высоты призмы равна 24. Найти (в градусах) угол при вершине основания (рис.7.3).
. Сумма длин этой диагонали и высоты призмы равна 24. Найти (в градусах) угол при вершине основания (рис.7.3).
|
|
|
 Решение. Дано:
Решение. Дано: 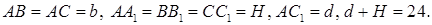
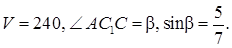 Найти
Найти 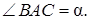
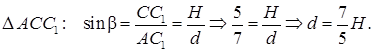
Решаем систему уравнений
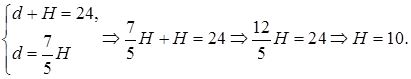 Тогда
Тогда 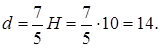 Из
Из 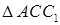 найдем
найдем 
Площадь основания призмы
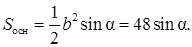
Объем призмы
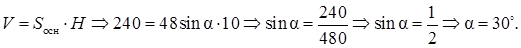
Ответ: 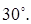
7.4 Основанием прямой призмы является прямоугольный треугольник ABC, у которого 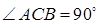 ,
, 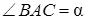 и катет
и катет 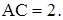 Диагональ боковой грани призмы, проходящей через гипотенузу AB, образует с боковой гранью, проходящей через катет AC, угол
Диагональ боковой грани призмы, проходящей через гипотенузу AB, образует с боковой гранью, проходящей через катет AC, угол 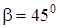 . Найти
. Найти  , если объем призмы равен
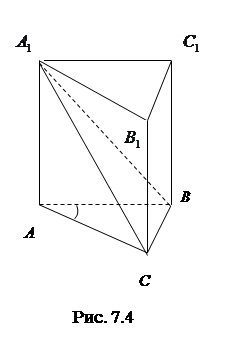
, если объем призмы равен 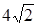 (рис.7.4).
(рис.7.4).
Решение. Дано:
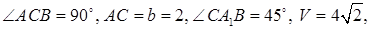
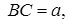
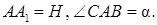
Найти 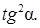
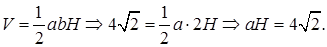
Согласно условию 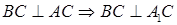 (по теореме о трех перпендикулярах), следовательно,
(по теореме о трех перпендикулярах), следовательно, 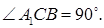 Далее,
Далее, 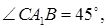 поэтому и
поэтому и 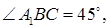 а это означает, что
а это означает, что 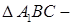 прямоугольный и равнобедренный, в нем
прямоугольный и равнобедренный, в нем 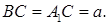

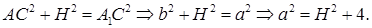
Решаем систему уравнений:
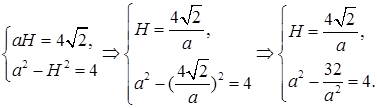
Во втором уравнении системы положим 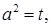 в результате чего уравнение приведется к виду
в результате чего уравнение приведется к виду
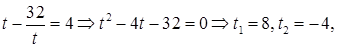
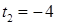 не удовлетворяет условию
не удовлетворяет условию 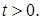
Получаем, что 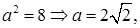 поэтому
поэтому
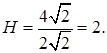
Из 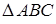 находим
находим
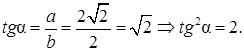
Ответ: 2.
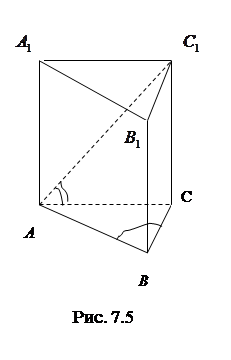
7.5 Основанием прямой призмы является равнобедренный тупоугольный треугольник. Диагональ боковой грани, противолежащей тупому углу основания, равна 6 и составляет с плоскостью основания угол 600. Найти (в градусах) тупой угол основания, если объем призмы равен 6,75 (рис 7.5).
Решение. Дано: 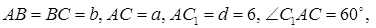
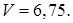 Найти тупой
Найти тупой 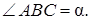
Объем призмы
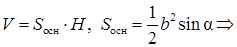
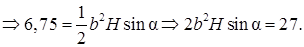
 поэтому
поэтому
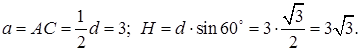
Следовательно,
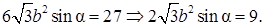
Далее, к треугольнику 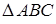 применим теорему косинусов:
применим теорему косинусов:
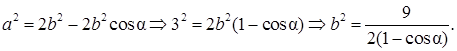
Тогда
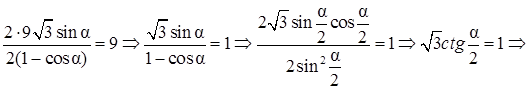
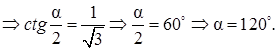
Ответ: 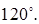
7.6 Основанием прямого параллелепипеда является ромб со стороной, равной 4, и острым углом 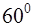 . Объем параллелепипеда равен 96. Найти (в
. Объем параллелепипеда равен 96. Найти (в
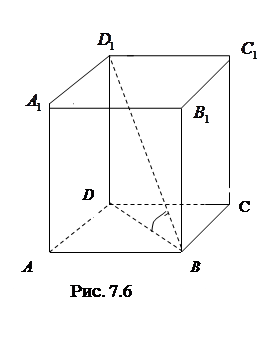 градусах) угол наклона меньшей диагонали параллелепипеда к плоскости основания (рис. 7.6).
градусах) угол наклона меньшей диагонали параллелепипеда к плоскости основания (рис. 7.6).
Решение. Дано:
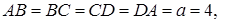
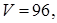
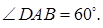 Найти
Найти 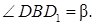
Объем призмы 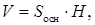 где
где 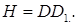 Найдем
Найдем 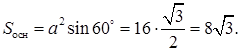
Тогда
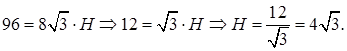
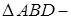 равносторонний, поэтому
равносторонний, поэтому 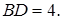
Из 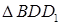 найдем
найдем
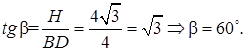
Ответ: 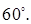
|
|
|
7.7 Основанием прямого параллелепипеда является квадрат. Длина бокового ребра равна 7. Найти (в градусах) угол между диагональю параллелепипеда и боковой гранью, если диагональ параллелепипеда равна 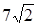 (рис. 7.7).
(рис. 7.7).
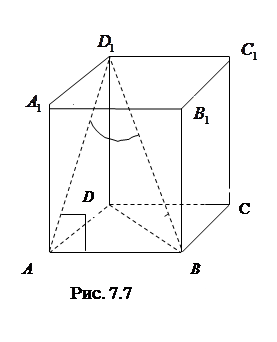 Решение. Дано:
Решение. Дано:
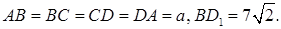
Найти 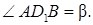
Из 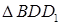 найдем
найдем 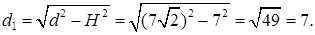
Из прямоугольного 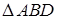 находим, что
находим, что
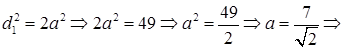
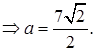
Рассмотрим 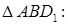
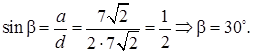
Ответ: 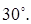
7.8 Основанием прямоугольного параллелепипеда является квадрат. Высота параллелепипеда равна 4. Сумма диагонали параллелепипеда и стороны основания равна 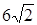 . Найти (в градусах) угол между диагональю параллелепипеда и его боковой гранью (рис. 7.8).
. Найти (в градусах) угол между диагональю параллелепипеда и его боковой гранью (рис. 7.8).
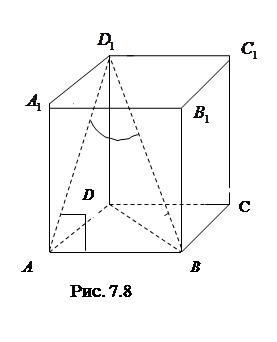 Решение. Дано:
Решение. Дано:
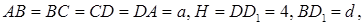
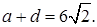
Найти 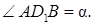
Диагональ квадрата 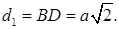
Из 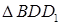 найдем
найдем 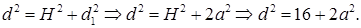 Решаем систему
Решаем систему
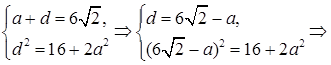
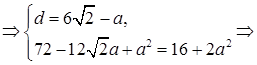
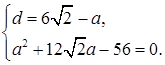
Решая квадратное уравнение, находим
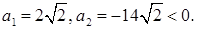
Тогда
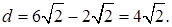
Из прямоугольного 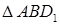 находим
находим
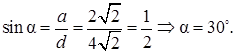
Ответ: 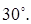
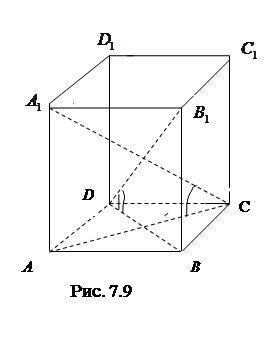 7.9 Основанием прямого параллелепипеда является ромб. Объем параллелепипеда равен 1,5 и его высота равна
7.9 Основанием прямого параллелепипеда является ромб. Объем параллелепипеда равен 1,5 и его высота равна 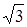 . Найти (в градусах) угол наклона к плоскости основания большей диагонали параллелепипеда, если его меньшая диагональ наклонена к плоскости основания под углом
. Найти (в градусах) угол наклона к плоскости основания большей диагонали параллелепипеда, если его меньшая диагональ наклонена к плоскости основания под углом  (рис. 7.9).
(рис. 7.9).
Решение. Дано:
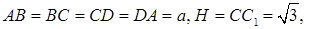
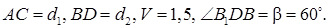
Найти 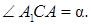

Так как диагонали ромба взаимно перпендикулярны, то 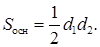
Из треугольников 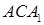 и
и 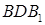 выразим диагонали
выразим диагонали 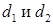 соответственно:
соответственно:
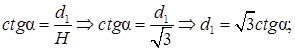
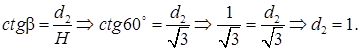
Следовательно,
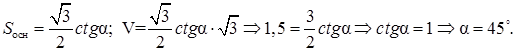
Ответ: 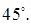
 2015-02-18
2015-02-18 1530
1530








