При разработке материалов городского населения методом случайного бесповторного отбора было установлено, что в городе А 15 % жителей старше 60 лет. Из общей численности населения города (500 тыс. человек) было отобрано 50 тыс. человек.
С вероятностью 0,683 определите предел, в котором находится доля жителей города А в возрасте старше 60 лет.
Рассчитаем среднюю ошибку выборочной доли:
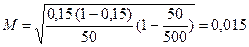 .
.
С вероятностью 0,683 предельная ошибка выборочной доли составит:
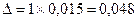 (или 4,8 %).
(или 4,8 %).
Определим верхнюю границу генеральной доли:
0,15 + 0,048 = 0,198 (или 19,8 %).
Определим нижнюю границу генеральной доли:
0,15 - 0,048 = 0,102 (или 10,2 %).
С вероятностью 0,683 можно утверждать, что доля жителей в возрасте старше 60 лет в городе А колеблется от 10,2 до 19,7 %:
10,2 % < P < 19,8 %
5. При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:
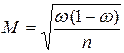 .
.
В практике проектирования выборочного наблюдения возникает потребность определения численности выборки, которая необходима для обеспечения определённой точности расчёта средних величин. Предельная ошибка выборки и её вероятность при этом является заданными.
6. Необходимая численность выборки при бесповторном случайном отборе для определения выборочной средней с определённой точностью вычисляется по формуле:
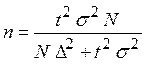 .
.
 2015-02-18
2015-02-18 2430
2430








