1.1 Первообразная, неопределенный интеграл
Определение. Функция F(x) называется первообразной функции f(x) на множестве X, если 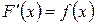 для всех
для всех 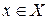 .
.
Выражение F(x)+C представляет собой семейство всех первообразных функции f(x). (C=const).
Определение. Если F(x) – одна из первообразных функции f(x), то выражение F(x)+C называется неопределенным интегралом.
Обозначается 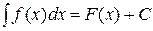 .
.
Простейшие свойства.
1) 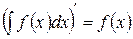
2) 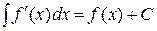
3) 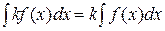
4) 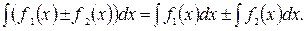
Таблица основных интегралов
1) 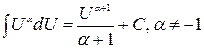 . .
| 10) 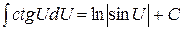 . .
|
2) 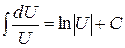 . .
| 11) 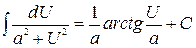 . .
|
3) 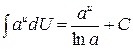 . .
| 12) 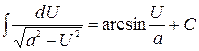 . .
|
4) 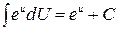 . .
| 13) 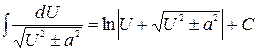 . .
|
5) 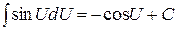 . .
| 14) 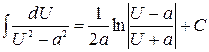 . .
|
6) 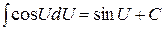 . .
| 15) 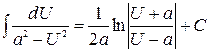 . .
|
7) 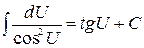 . .
| 16) 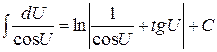 . .
|
8) 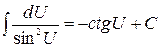 . .
| 17) 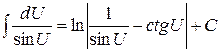 . .
|
9) 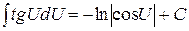 . .
|
В частности:
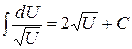 ;
; 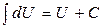 ;
; 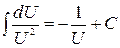 .
.
Из определения и свойств неопределенного интеграла следует, что дифференцирование и интегрирование являются взаимно обратными действиями: производная правой части в каждой формуле равна подынтегральной функции. Проверим, например, формулу 2.
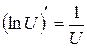
Примеры:
1) 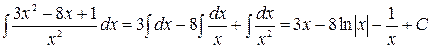 ;
;
2) 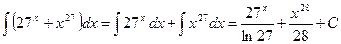 .
.
 2015-02-18
2015-02-18 264
264







