Дифференциальные уравнения 1 порядка

ДУ первого порядка называется уравнение, связывающее независимую переменную, искомую функцию и ее первую производную:

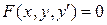
или в явном виде

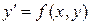
(1)

Теорема Коши. Если в уравнении (1) функции 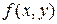, 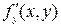определены и непрерывны в некоторой области изменения переменных x и y, то какова бы ни была внутренняя точка 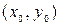этой области, ДУ имеет единственное решение y=y(x), удовлетворяющее начальным условиям

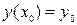
(2)

Геометрически это означает, что через каждую внутреннюю точку 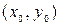проходит единственная интегральная кривая.

Определение. Функция y=y (x, С), зависящая от аргумента и произвольной постоянной С, называется общим решением ДУ, если

1) при любых значениях С функция y =y (x, С) является решением уравнения (1);

2) Какова бы ни была точка 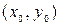, существует единственное значение постоянной 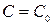такое, что 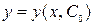– есть решение (1), удовлетворяющее начальным условиям (2).