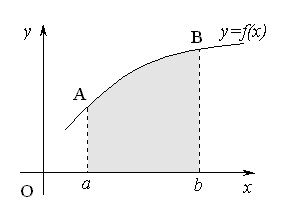
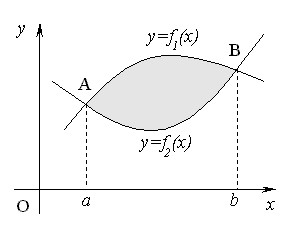
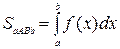Вычисление площадей плоских фигур. – площадь криволинейной трапеции

– площадь криволинейной трапеции.

Площадь фигуры, ограниченной линиями 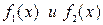, находим по формуле

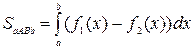
Эта формула остается справедливой при любом расположении рассматриваемой фигуры.

Пример (см. задание 3):

Вычислить площадь фигуры, ограниченной линиями: , .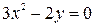

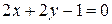1) Найдем точки пересечения данных кривых.

;

;

;

; .

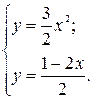
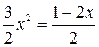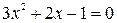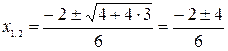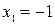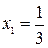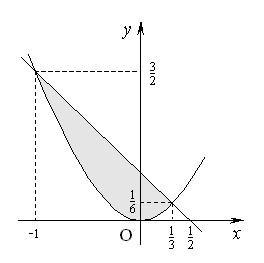
2) Построим графики данных функций.

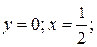
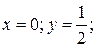(для прямой )

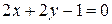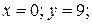
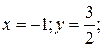
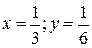(парабола ).

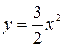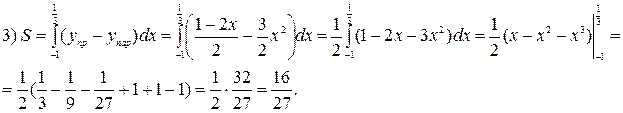4 Дифференциальные уравнения