Пусть функции f (x 1, x 2, …, xn) и Fi (x 1, x 2, …, xn) (i = 1,2, …,k) дифференцируемы в некоторой области D М Rn. Тогда задача отыскания точек условного экстремума функции f (x 1, x 2, …, xn) при условиях связи
|
эквивалентна задаче о нахождении точек обычного (безусловного) экстремума функции Лагранжа:
|
| (4) |
Схема метода Лагранжа:
1. Составляем функцию Лагранжа (4).
2. Для отыскания стационарных точек функции Лагранжа находим ее частные производные по всем аргументам
 и приравниваем их к нулю. Получаем систему (n + k) уравнений с (n + k) неизвестными: и приравниваем их к нулю. Получаем систему (n + k) уравнений с (n + k) неизвестными: |
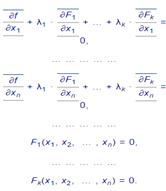
Если (x10,:::,xn0; λ10,:::,λk0) — решение этой системы, то оно определяет стационарную точку (x10,:::,xn0) функции f(x1,x2,:::,xn) при условиях связи (2), в которой функция может иметь условный экстремум.
3. Чтобы установить наличие или отсутствие условного экстремума в каждой стационарной точке M0, нужно исследовать знак 2–го дифференциала функции Лагранжа
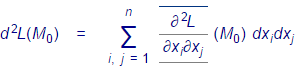
при значениях дифференциалов dx 1, …,dxn, не равных одновременно нулю и удовлетворяющих продифференцированным уравнениям связи
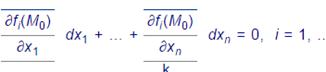
Геометрический смысл условного экстремума функции: Условными экстремумами функции z = f(x,y) при F(x,y) = 0 являются ее экстремумы на линии, образующейся в сечении поверхности z = f(x,y) цилиндрической поверхностью F(x,y) = 0.
9. Определение двойного интеграла. Его свойства. Вычисление двойного интеграла в декартовой системе координат
Определение:
Двойным интегралом от функции 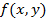 по ограниченной замкнутой области
по ограниченной замкнутой области 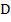 называется предел интегральной суммы, построенной для функции
называется предел интегральной суммы, построенной для функции 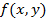 при неограниченном увеличении числа разбиений области
при неограниченном увеличении числа разбиений области 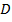 на ячейки (
на ячейки ( 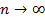 ) и при стягивание каждой ячейки в точку (
) и при стягивание каждой ячейки в точку ( 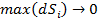 ), если такой предел существует и не зависит от способа разбиения области
), если такой предел существует и не зависит от способа разбиения области 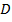 на ячейки, ни от выбора
на ячейки, ни от выбора 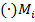 в каждой из них.
в каждой из них.
Теорема существования:
Для всякой непрерывной функции 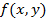 в ограниченной замкнутой области
в ограниченной замкнутой области 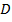 существует двойной интеграл:
существует двойной интеграл: 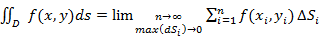
Свойства двойного интеграла:
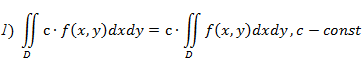
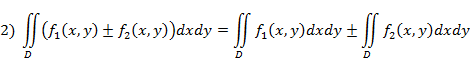
3) Если область 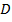 разбить линией на две области
разбить линией на две области 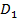 и
и 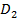 такие, что
такие, что 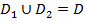 , а пересечение
, а пересечение 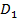 и
и 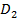 состоит лишь из линии, их разделяющей, то:
состоит лишь из линии, их разделяющей, то:
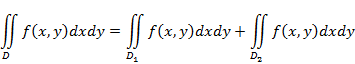
4) Если в области 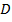 имеет место неравенство
имеет место неравенство 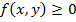 , то и
, то и 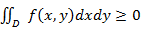 . Если в области
. Если в области 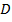 функции
функции 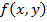 и
и 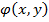 удовлетворяют неравенству, то и
удовлетворяют неравенству, то и 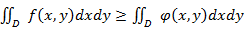
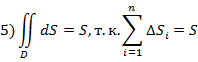
6) Если функция 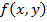 непрерывна в замкнутой области
непрерывна в замкнутой области 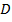 , площадь которой
, площадь которой 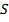 , то
, то 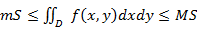 , где
, где 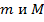 – соответственно наименьшее и наибольшее значения подынтегральной функции в области
– соответственно наименьшее и наибольшее значения подынтегральной функции в области 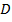 .
.
7) Если функция непрерывна в замкнутой области 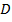 , площадь которой
, площадь которой 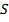 , то в этой области существует такая точка
, то в этой области существует такая точка 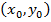 , что
, что 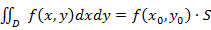 . Величину
. Величину 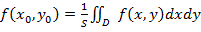 называют средним значением функции
называют средним значением функции 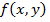 в области
в области 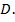
Пример вычисления:
Вычислить 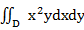 в области
в области 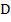 , ограниченной кривыми
, ограниченной кривыми 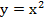 и
и 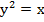 .
.

 2015-02-04
2015-02-04 1011
1011








