Остаток ряда и его оценка

Рассмотрим сходящийся числовой ряд

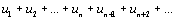(23)

Вычисление суммы ряда S = 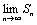обычно технически очень сложно. Поэтому в качестве S берут S ≈ S_n. Точность этого равенства возрастает с увеличением n.

Определение 7. Если числовой ряд сходится, то разность R_n = S - S_n называется n -м остатком ряда.

Таким образом, R_n представляет собой сходящийся числовой ряд:

R_n = u_n+1+u_n+2+….

Заметим, что 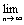R_n= 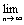(S-S_n)=S-S=0.

Абсолютная погрешность при замене суммы ряда S его частичной суммой S_n равна | R_n|=|S-S_n|. Таким образом, если требуется найти сумму ряда с точностью до E >0, то надо взять сумму такого числа n первых членов ряда, чтобы выполнялось условие | R_n|<E. Однако в общем случае находить точно R_n не удаётся.

Теорема 11. (Об оценке остатка знакочередующегося числового ряда)

Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n -й остаток по абсолютной величине не превосходит модуля (n +1)-го члена ряда.

Доказательство. Пусть ряд u₁-u₂+u₃-u₄+…+(-1)^n-1.u_n+… сходится по признаку Лейбница. Тогда n -й остаток ряда R_n=±(u_n+1-u_n+2+u_n+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |R_n|≤|u_n+1 |. Теорема доказана.

Пример. Вычислить с точностью до 0,01 сумму ряда 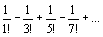Очевидно, ряд сходится по признакуЛейбница. u₁ = 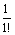=1; u₂ = 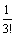≈ ≈0,166; u₃ = 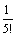≈0,008<0,01. Поэтому S ≈1-0,166≈0,84.

23. Абсолютно и условно сходящиеся числовые ряды. Теорема об абсолютной сходимости числового ряда. Использование признаков сходимости положительных рядов для исследования сходимости знакопеременных рядов.