Рассмотрим функцию 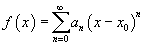 . Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
. Ее областью определения является множество тех значений x, при которых ряд сходится. Область определения такой функции называется интервалом сходимости.
Если интервал сходимости представляется в виде 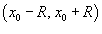 , где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
, где R > 0, то величина R называется радиусом сходимости. Сходимость ряда в конечных точках интервала проверяется отдельно.
Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле
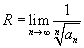
или на основе признака Даламбера:
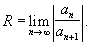
Теорема Абеля. Если степенной ряд (1.2) сходится при некотором 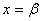 , где
, где 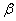 -число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что
-число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что 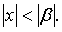 Наоборот, если ряд (12) расходится при
Наоборот, если ряд (12) расходится при 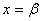 , то он расходится при всех значениях x таких, что
, то он расходится при всех значениях x таких, что 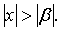
 2015-02-04
2015-02-04 784
784








