Абсолютная сходимость:
Теорема (первый признак сравнения). Даны числовые ряды 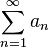 и
и 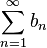 , где
, где 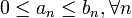
Тогда:
1. Если ряд 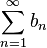 - сходится, то
- сходится, то 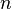 ряд
ряд 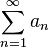 сходится.
сходится.
2. Если ряд 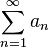 - расходится, то и ряд
- расходится, то и ряд 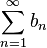 расходится.
расходится.
Теорема (второй признак сравнения). Даны числовые ряды 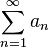 ,
, 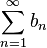 ,
, 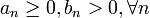
Пусть 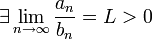 , тогда ряды сходятся или расходятся одновременно.
, тогда ряды сходятся или расходятся одновременно.
Теорема (признак Даламбера). Дан ряд 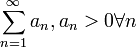 . Пусть
. Пусть 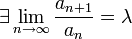 , тогда
, тогда
1. Если 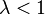 - ряд сходится
- ряд сходится
2. Если 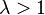 - ряд расходится
- ряд расходится
Теорема (Признак Коши). Дан ряд 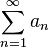 ,
, 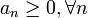 . Пусть
. Пусть 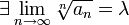
тогда:
1. Если 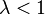 ряд сходится;
ряд сходится;
2. Если 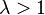 ряд расходится.
ряд расходится.
Теорема (Интегральный признак Коши). Пусть функция 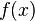 определена на
определена на 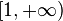 , неотрицательна на
, неотрицательна на 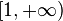 и
и 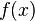 монотонно не возрастает на
монотонно не возрастает на 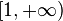 . Тогда ряд
. Тогда ряд 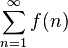 и интеграл
и интеграл 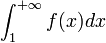 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Условная сходимость:
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.
Или в два пункта:
1) Ряд является знакочередующимся. Если аn >0 при всех n =1,2,3…
2) Члены ряда убывают по модулю: 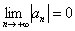 . Причём, убывают монотонно.
. Причём, убывают монотонно.
Если выполнены оба условия, то ряд сходится.
Если ряд 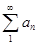 сходится, то
сходится, то 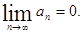
Обратно, если 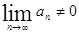 либо не существует, то ряд расходится.
либо не существует, то ряд расходится.
Функциональный ряд и его область сходимости. Степенные ряды. Теорема Абеля, радиус и интервал сходимости степенного ряда. Почленное дифференцирование и интегрирование степенных рядов.
Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция 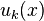 .
.
Область сходимости ряда. Так называют множество точек сходимости функционального ряда, т.е. множество значений аргумента х, для которых ряд (бесконечная сумма)
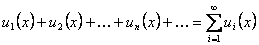 сходится.
сходится.
Определение
Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
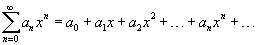
Часто рассматривается также ряд, расположенный по степеням (x − x 0), то есть ряд вида
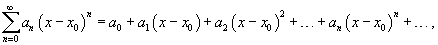
где x 0 − действительное число.
 2015-02-04
2015-02-04 933
933








