2015-02-24
345
(пласт однородный изотропный пористый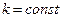 
)
однородной невесомой жидкостью вязкости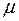 
заполнены поры пласта
режим ламинарный жесткий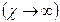 
или установившийся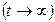 
Простейшее решение этой задачи базируется на следующих предпосылках:
а) однородный изотропный пористый, трещиноватый или трещиновато-пористый пласт проницаемостью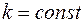 
ограничен непроницаемыми плоскостям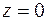и 
и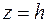 
(кровля и подошва пласта) и проницаемыми цилиндрическими поверхностями 
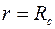(стенка скважины), 
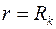(поверхность питания), на которых поддерживаются однородные граничные условия
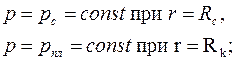
| (3.55) |
б) поры пласта заполнены однородной невесомой жидкостью вязкости ;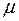
в) фильтрация происходит при жестком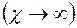 
или установившемся 
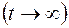ламинарном режиме.
Основные уравнения теории фильтрации в этом случае запишутся в виде
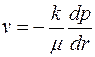
| (3.56) |
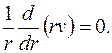
| (3.57) |
Подстановка (3.56) в (3.57) дает простейший вид уравнения Лапласа
|
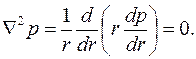
Общим решением этого уравнения является функция
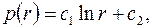
| (3.58) |
где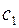 
и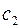 
– постоянные интегрирования, определяемые граничными условиями (3.55).
|
|
|
В результате получим решение первой основной граничной задачи фильтрации (3.55 – 3.57):
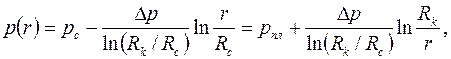
| (3.59) |
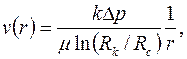
| (3.60) |
где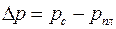 
– заданный перепад давления между скважиной и пластом.
При поглощении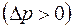 
проявлении 
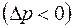пласта объемный расход жидкости через любую цилиндрическую поверхность 
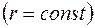, в том числе и через стенку скважины,
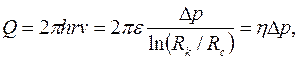
| (3.61) |
где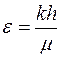 
; 
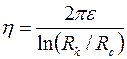– соответственно коэффициент гидропроводности, или просто гидропроводность, и коэффициент продуктивности, или просто продуктивность пласта; размерность м3/Па.с.
Формула (3.61) впервые получена французским инженером Дюпюи и поэтому названа его именем.
