2015-02-24
397
Для множества с n =5 элементами число всех упорядоченных разбиений, содержащих k =2 подмножества равно S 5,2. По таблице чисел Стирлинга 2-го рода находим S 5,2= 15.
Ответ на п. 3 задания 15: S 5,2= 15, где S 5,2- число Стирлинга 2-го рода из 5 по 2.
4 ) Решение п. 4 задания 15.
Для множества с n =5 элементами число всех упорядоченных разбиений, содержащих k =2 подмножества равно S 5,2. Число перестановок без повторений для k подмножеств равно k!=2! По таблице чисел Стирлинга 2-го рода находим S 5,2= 15. По таблице факториалов находим 2!=2.
Ответ на п. 4 задания 15:2! S 5,2=2×15= 30, где S 5,2 - число Стирлинга 2-го рода из 5 по 2, 2! – факториал числа «2».
Табл. Числа разбиений Рп m
| Рп m | m = 1 | ||||||||||||
| n =1 | |||||||||||||
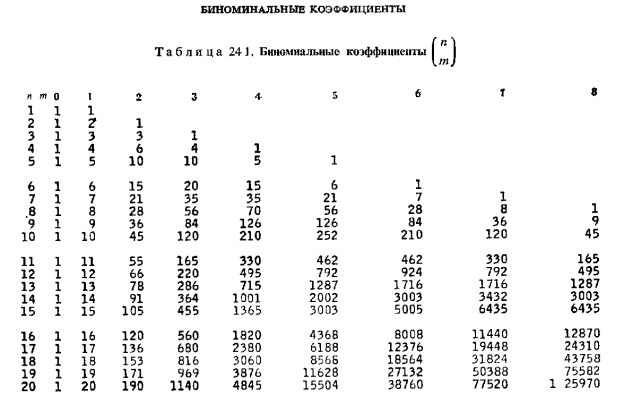
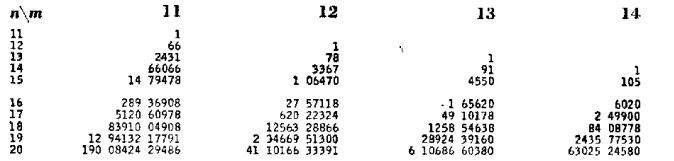
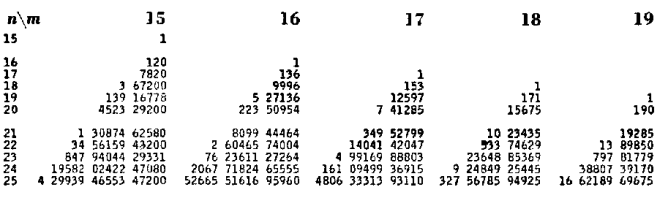
Табл. Биномиальные коэффициенты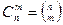 
(треугольник Паскаля)
| m =0 | |||||||||
| n = | |||||||||
| 2 | 2 | ||||||||
| 5 | |||||||||
| 6 | б | ||||||||
