Свойства функции распределения

1. ;

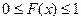2. ;

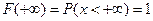3. ;

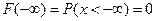4. 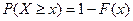- вероятность противоположного события;

5. 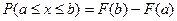- вероятность попадания в интервал значений.

6.

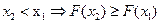
Плотность вероятности

(дифференциальный закон) распределения непрерывной с.в.

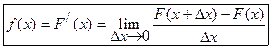
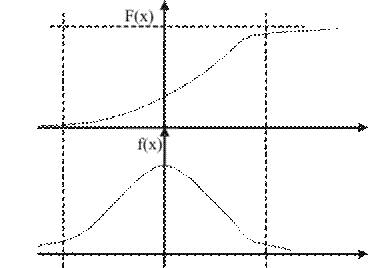
Свойства плотности вероятности

1. ;

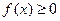2. 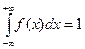- условие нормировки (единичная площадь под кривой распределения, полнота группы событий);

3. 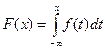- выражение функции распределения через плотность;

4. 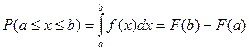- вероятность попадания в интервал значений.

Функции 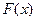, , 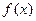ряды распределения 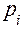исчерпывающим образом описывают одномерную с.в., однако они довольно сложны, а информация, содержащаяся в них, зачастую избыточна, поэтому широко используют числовые характеристики.