2015-03-22
779
Задача такого рода очень часто встречается в практике производственных процессов, когда регламентируемый допуск на какую-либо характеристику качества меньше рассеяния этой характеристики, обеспечиваемой существующим технологическим регламентом. Тогда может возникать вопрос о целесообразности такого процесса - может быть, потери от брака превышают выгоды от реализации годной продукции? Такая чисто экономическая задача может быть правильно решена только с использованием вероятностных статистических методов, а "исходным материалом" для её решения является точно рассчитанная вероятность производства годной или, наоборот, бракованной продукции. Эффективным средством определения такой вероятности может стать программа MS EXCEL.
Пример. Чертежом задан размер детали -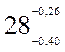 
мм. После пробной обработки пяти деталей контролировали этот размер со следующими результатами: 27,64; 27,58; 27,65; 27,55; 27,60.
Определить вероятность обеспечения регламентируемой точности при существующих условиях производства и настройки процесса.
Решение.
1. По результатам контроля выборки определяются точечные оценки рассеяния генеральной совокупности этого размера, в частности, среднее значение (функция СРЗНАЧ), выборочное СКО (функция СТАНДОТКЛОН).
2. Делается предположение, что рассеяние размера подчиняется нормальному закону распределения (при большем объёме выборки и сомнении в данном предположении его можно проверить с использованием функции ХИ2ТЕСТ).
3. С использованием функции НОРМРАСП (см. рис. 4.8) определяется интегральная функция нормального распределения F(x) для интервала (x1, x2), где x1 = 27,6 мм - нижняя, а x2 = 27,74 мм - верхняя граница поля допуска. Выражение F(x) в процентах и представляет собой искомую вероятность обеспечения регламентируемой точности. Для вычисления F(x) для данного интервала в соответствии с рекомендациями, приведёнными в §4.4, последовательно выполняют следующие действия:
- определяют интегральную функцию разность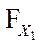 
, подставляя в аргументы функции НОРМРАСП рассчитанные «Среднее» и «Стандартное откл», в «Интегральная» - значение ИСТИНА, а в «x» - x1. (Вносят в аргументы сами предварительно рассчитанные значения или ссылки на ячейки, содержащие результаты расчётов).
- определяют интегральную функцию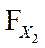 
, повторяя расчёт, но в аргумент «x» вместо x1 подставляют величину x2,
- вычисляют разность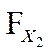 
- 
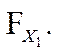
Результаты расчётов представлены в табл. 6.2.
Таблица 6.2. Результаты расчётов вероятности обеспечения регламентируемой точности при существующих условиях производства и настройки процесса
| Среднее | 27,61 |
| Выборочное СКО | ≈ 0,043 |
Интегральная функция нормального распределения для нижней границы поля допуска 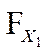 | ≈ 0,408 |
Интегральная функция нормального распределения для верхней границы поля допуска 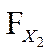 | ≈ 0,99875 |
| Разность 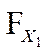- 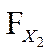| ≈ 0,591 |
По результатам расчёта видно:
- «центр настройки» (выборочное среднее, 27,61 мм) смещён относительно середины поля допуска (27,67 мм) в сторону его нижней границы допуска.
- при существующих условиях производства и настройки процесса ~ 40 % производимой продукции должно попадать в брак.
Естественно предполагать, что при нормальном распределении контролируемого параметра (в нашем случае - размера) правильный выбор центра настройки (посередине поля допуска) должен увеличить вероятность производства годной продукции.
