2015-03-22
751
Задание 1. Составить интерполяционный многочлен Ньютона для функции, заданной таблицей1.1
| x | |||||
| y |
1.2
| x | |||||
| y |
Задание 2. Известны значения некоторой функции f(x) в отдельных точках. Пользуясь интерполяционной формулой Ньютона, вычислите f(2,3):
2.1 f(1)=1,00; f(2)=0,25; f(3)=0,11; f(4)=0,06; f(5)=0,04; f(6)=0,03; f(7)=0,02
2.2 f(1)=2,00; f(2)=0,50; f(3)=0,22; f(4)=0,125; f(5)=0,08; f(6)=0,06; f(7)=0,04
Задание 3.
3.1 Некоторая функция f(x) задана таблицей.
| x | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| y | 0,095 | 0,182 | 0,262 | 0,336 | 0,405 | 0,470 |
Вычислите первую производную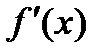 
и вторую производную 
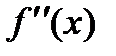данной функции в точке x=1,22.
3.2 Некоторая функция f(x) задана таблицей.
| x | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| y | 0,693 | 0,788 | 0,875 | 0,956 | 1,030 | 1,099 | 1,163 |
Вычислите первую производную 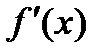и вторую производную 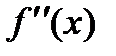данной функции в точке x=1,22.
Вопросы для самоконтроля
- Что называется интерполяцией.
- В каких случаях используют интерполяционные формулы?
- Как определить точность вычислений?
- Зная квадраты чисел 5,6,7,8, найдите квадрат числа 6,25, используя формулы Ньютона, и проверьте результат с помощью калькулятора.
|
|
|
