Для понимания физики явления, полезно рассмотреть самый простой случай вариационного метода, когда 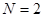 . Это значит, что пробная волновая функция
. Это значит, что пробная волновая функция 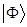 представляется в виде двух слагаемых:
представляется в виде двух слагаемых:
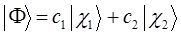
Базисные функции 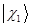 и
и 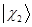 могут отвечать различным физическим ситуациям. Например,
могут отвечать различным физическим ситуациям. Например, 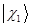 описывает движение электронов в некоторой области
описывает движение электронов в некоторой области 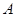 , а
, а 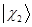 - в области
- в области 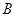 . На практике
. На практике 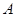 и
и 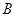 могут означать два разных атома, две области в молекуле и т.д. Такая модель называется двухуровневым приближением и часто используется в физике и квантовой химии. Так, по - определению имеем:
могут означать два разных атома, две области в молекуле и т.д. Такая модель называется двухуровневым приближением и часто используется в физике и квантовой химии. Так, по - определению имеем:
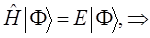
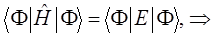
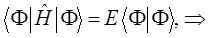
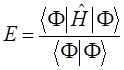
Подставляя в полученное уравнение для средней энергии разложение пробной волновой функции по базисному набору соответствующих базисных функций 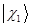 и
и 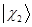 , будем иметь соответственно:
, будем иметь соответственно:
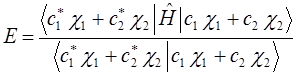
на основании теоремы о не взаимодействии, согласно которой «если система состоит из двух или нескольких невзаимодействующих подсистем, то её полная волновая функция 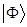 равна произведению волновых функций отдельных подсистем
равна произведению волновых функций отдельных подсистем 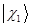 ,
, 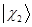 ,
, 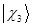 , …,
, …, 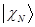 , а энергия – сумме энергий подсистем
, а энергия – сумме энергий подсистем 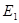 ,
, 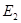 ,
, 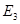 , …,
, …, 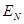 »:
»:
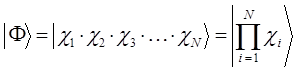
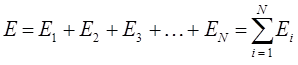
а также учитывая, что:
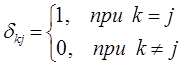
будем иметь соответственно после раскрытия скобок:
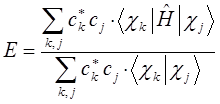
или для рассматриваемого случая:
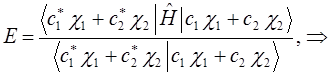
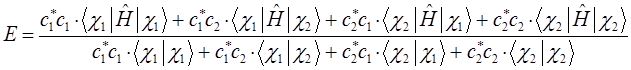
введём следующие обозначения:
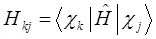
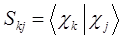
или для нашего случая:
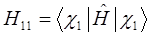
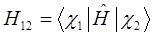
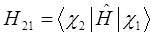
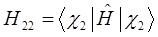
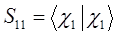
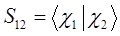
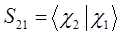
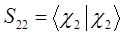
с учётом введенных выше обозначений, выражение для средней энергии:
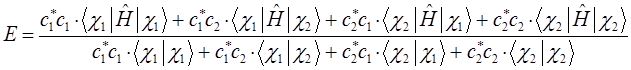
можно будет представить к виду:
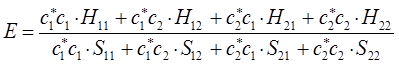
или в общем виде:
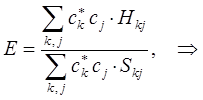
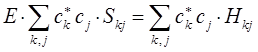
т.е. имеем соответственно:
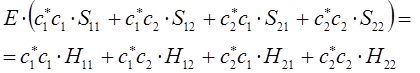
вариационные коэффициенты найдём из условия вида:
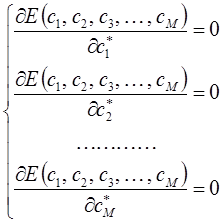
Дифференцируя полученное выражение (в общем виде) по коэффициенту 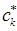 :
:
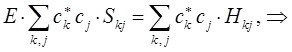
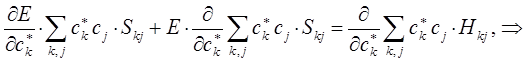
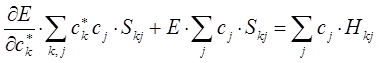
имеем для нашего случая:
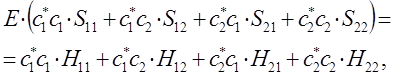
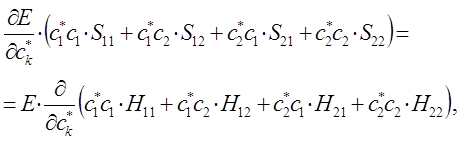
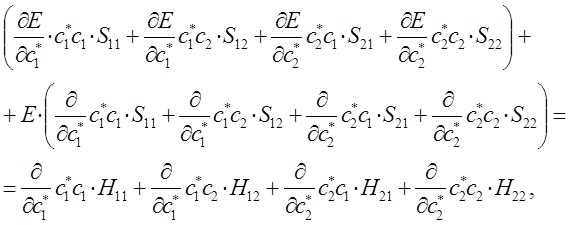
а так как производная от энергии по вариационному коэффициенту равна нулю в точке экстремума:
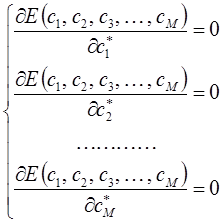
тогда:
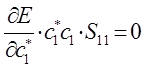
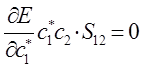
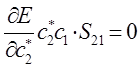
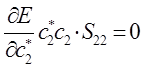
или в общем виде:
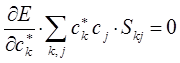
Полученное в ходе дифференцирования выражение:
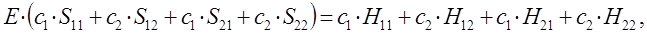
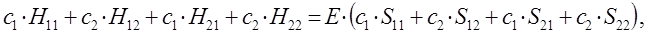
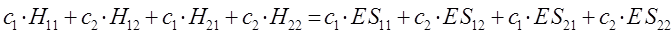
можно будет далее разделить на два линейных уравнения вида:
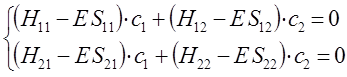
или в общем виде:
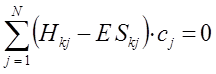
Полученная в ходе проделанных выше выкладок система уравнений, может быть далее задана в матричном виде:
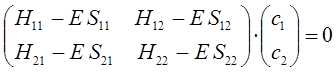
Данная система представляет собой систему линейных однородных уравнений. Из теории линейных уравнений известно, что такая система имеет нетривиальное решение при условии, что детерминант, составленный из коэффициентов при неизвестных (неизвестными являются вариационные коэффициенты), равен нулю:
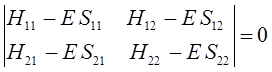
Учитывая свойство эрмитовости гамильтониана и ортонормированность базисных функций 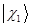 и
и 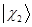 , будем иметь соответственно для диагональных и недиагональных элементов:
, будем иметь соответственно для диагональных и недиагональных элементов:
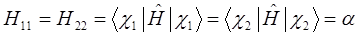
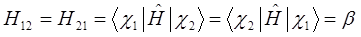
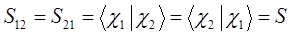
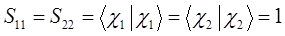
здесь матричные элементы определителя:
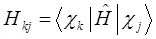
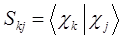
представляют собой интегралы, имеющие размерность энергии: 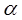 - кулоновский интеграл;
- кулоновский интеграл; 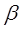 - обменный (резонансный) интеграл и
- обменный (резонансный) интеграл и 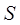 - интеграл перекрывания.
- интеграл перекрывания.
Итак, в ходе преобразований мы пришли к определителю вида:
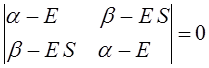
Раскрывая определитель и решая получившееся квадратное уравнение, получаем два значения для энергии, соответствующие симметричному и несимметричному решениям:
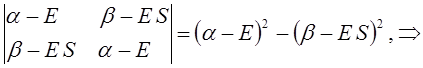
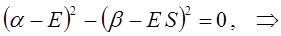
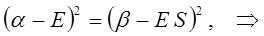
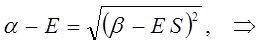
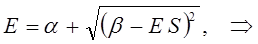
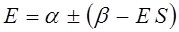
раскрывая скобки в полученном выражении, имеем:
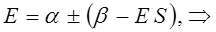
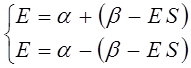
Рассмотрим уравнение вида:
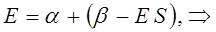
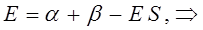
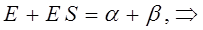
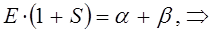
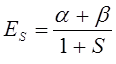
аналогично получаем:
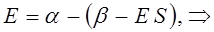
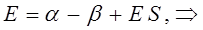
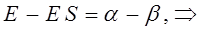
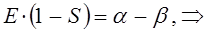
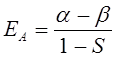
Составим уравнение для нахождения вариационных коэффициентов. Из полученной выше системы линейных уравнений:
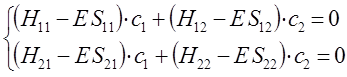
с учётом приведенных выше соображений следует, что:
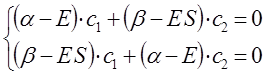
Коэффициенты 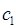 и
и 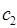 можно получить, если подставить найденные значения энергии в полученную в ходе преобразований систему. Однако необходимо заметить, что из двух однородных уравнений нельзя получить три неизвестных
можно получить, если подставить найденные значения энергии в полученную в ходе преобразований систему. Однако необходимо заметить, что из двух однородных уравнений нельзя получить три неизвестных 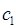 ,
, 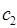 и
и 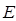 , а лишь одно из них и отношение двух других. Найдя
, а лишь одно из них и отношение двух других. Найдя 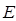 , мы можем теперь получить отношение величин
, мы можем теперь получить отношение величин 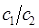 . Итак, в ходе преобразований, система линейных однородных уравнений:
. Итак, в ходе преобразований, система линейных однородных уравнений:
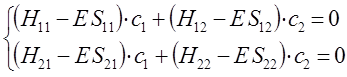
была преобразована нами к виду:
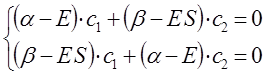
Из первого уравнения:
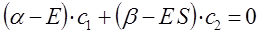
следует, что:
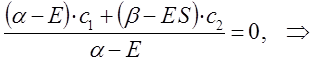
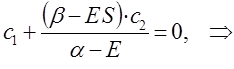
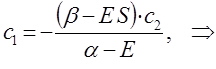
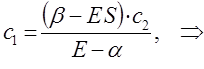
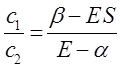
учитывая, что:
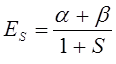
будем иметь соответственно:
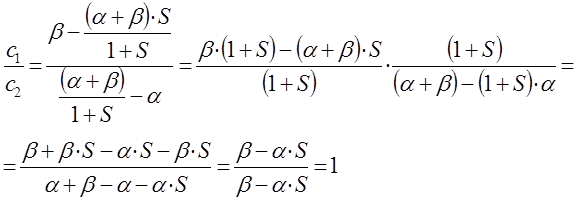
таким образом, имеем соотношение:
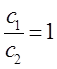
которое может быть преобразовано далее к виду:
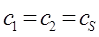
Аналогичные преобразования проведём и над вторым уравнением:
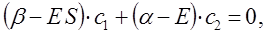
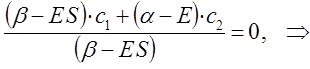

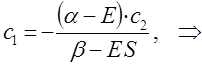
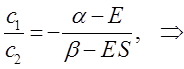
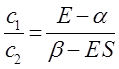
учитывая, что:
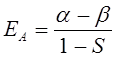
будем иметь соответственно:
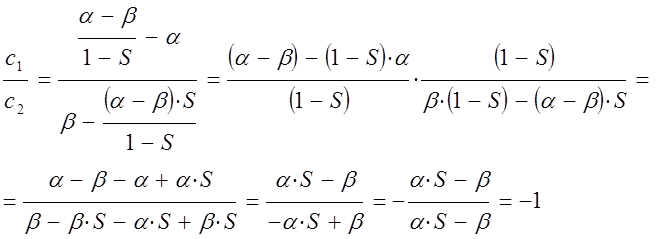
таким образом, имеем соотношение:
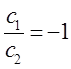
которое может быть преобразовано далее к виду:
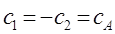
подстановка значений:
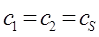
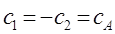
в разложение пробной волновой функции 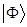 по базисному набору
по базисному набору 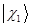 и
и 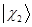 :
:
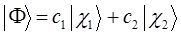
приводит к двум решениям – симметричному и ассиметричному, вида:
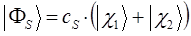
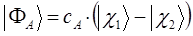
Для определения самих коэффициентов 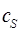 и
и 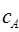 , воспользуемся условием нормировки:
, воспользуемся условием нормировки:
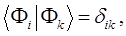
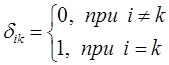
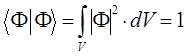
подставим сюда выражение для 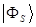 :
:
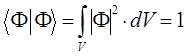
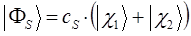
имеем таким образом:
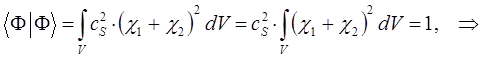
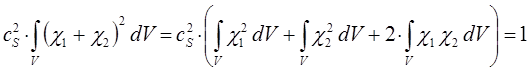
учитывая, что:
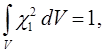

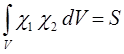
имеем:
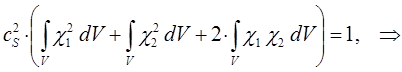
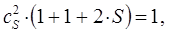
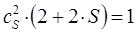
или в окончательном виде:
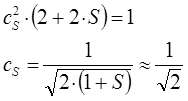
Аналогичным образом получим выражение и для коэффициента 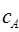 :
:
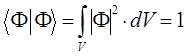
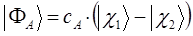
после соответствующих преобразований, получаем выражение вида:
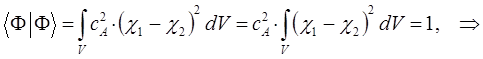
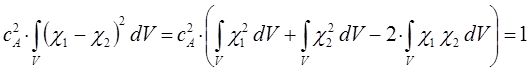
учитывая также, что:
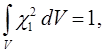

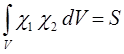
имеем:
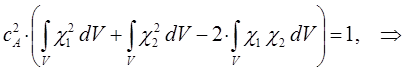
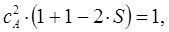
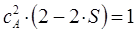
или в окончательном виде:
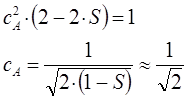
Таким образом, в ходе проделанных выкладок, приходим соответственно к выражениям для энергий и соответствующих им волновых функций симметричного и антисимметричного состояний квантово-механической системы:
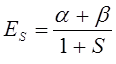
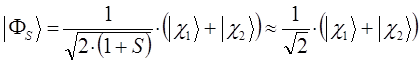
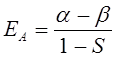

как это следует из решений уравнения Шрёдингера, эти орбитали ортогональны:
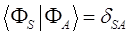
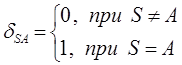
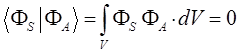
в этом легко убедиться:
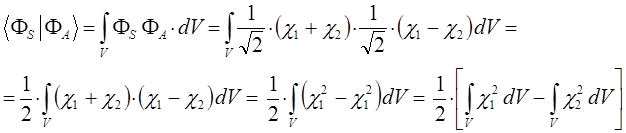
поскольку по определению:
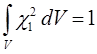
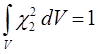
тогда соответственно:
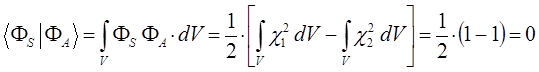
и таким образом:
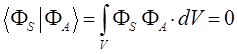
 2015-03-22
2015-03-22 1581
1581