Вариационные принципы механики. Вариационная теорема

В квантовой механике вариационный метод является методом нахождения приближённых волновых функций и соответствующих им энергий. Представим энергию квантово-механической системы как функционал. Для этого уравнение Шрёдингера:

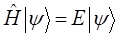
умножим слева на бра-вектор 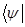, получим:

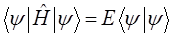
Отсюда следует выражение для энергии системы:

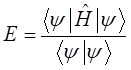
Если волновые функции 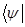нормированы, то полученное выражение может быть представлено к виду:

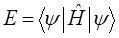
Как правило, точные волновые функции, удовлетворяющие уравнению Шрёдингера:

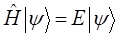
неизвестны, поэтому в качестве приближённой волновой функции можно выбрать какую-либо функцию 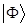, которая по физическим соображениям может оказаться достаточно корректной. Такую волновую функцию 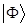называют пробной функцией. Предположим, что для некоторой квантово-механической системы с гамильтонианом 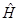точные собственные значения (энергии) пронумерованы в порядке возрастания: 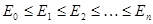и им соответствуют собственные функции: 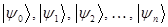. Наименьшее собственное значение 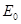представляет собой энергию основного состояния. Среднее значение энергии системы, в общем случае, можно вычислить с любой произвольной функцией. Тогда энергия, вычисленная с пробной функцией 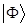, не будет ниже энергии основного состояния, т.е.

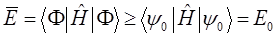
или в компактной форме:

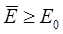
В силу данного неравенства, среднее значение энергии, вычисленное с пробной функцией 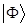, будет определять верхнюю границу для основного состояния рассматриваемой квантово-механической системы. Данное неравенство называют также вариационным неравенством. Для доказательства данного неравенства, разложим пробную волновую функцию 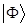в ряд по собственным функциям гамильтониана:

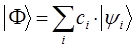
поскольку коэффициенты 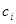в данном разложении представляют собой комплексные величины, то сопряжённый бра-вектор 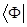будет иметь вид:

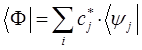
Подставив значения бра- и кет-векторов в формулу для среднего значения, будем иметь соответственно:

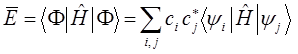
Учитывая, что векторы 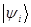являются собственными векторами оператора 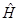, полученное выше выражение можно переписать в виде:

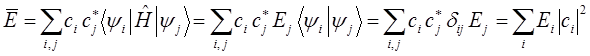
или учитывая вариационное неравенство:

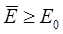
будем иметь соответственно:

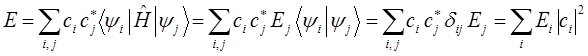
Запишем условие нормировки пробной волновой функции:

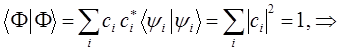
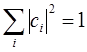
Умножим теперь данное выражение на :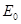

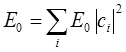
и вычислим разность энергий:

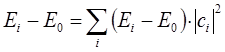
Поскольку 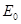соответствует основному состоянию и имеет минимальное значение среди всех значений 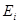, то выполняется неравенство:

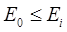
Очевидно также, что квадраты коэффициентов удовлетворяют условию:

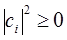
тогда из выражения вида:

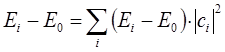
следует неравенство:

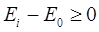
Из вариационного неравенства следует, что чем точнее 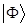аппроксимирует 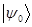, т.е. чем ближе пробная функция к точной, 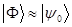, тем точнее среднее значение энергии, вычисленное с пробной функцией, 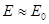. В общем случае пробная функция может зависеть от ряда параметров, называемых вариационными параметрами 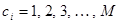, т.е. 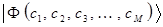. Тогда вариационная задача будет сводиться к нахождению таких значений параметров 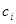, при которых среднее значение энергии, вычисленное с пробной функцией:

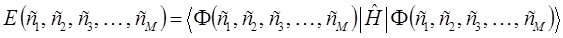
будет достаточно близким к точному собственному значению гамильтониана.

Конкретные численные значения параметров находят из условий вида:

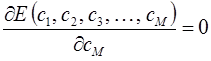
Процедура нахождения вариационных параметров 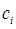, при которых энергия будет иметь минимальное значение, называется минимизацией энергии.