Построить эпюру продольных сил для бруса, если :
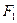 = F;
= F; 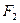 = 2F,
= 2F, 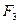 =4F.
=4F.
Решение. Разбиваем брус на участки, начиная со свободного конца. Границами участков являются сечения, в которые приложены внешние силы. Применяя метод сечений, оставляем правую часть (левую отбрасываем) – это позволяет не определять реакцию заделки.
Проводя произвольно сечение а-а на участке I, составляем уравнение равновесия:
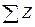 = 0 F -
= 0 F - 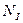 = 0
= 0
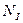 = F (растяжение)
= F (растяжение)
Проводим сечение в-в на участке II:
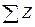 =
= 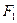 -
- 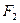 -
- 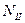 = F- 2F-
= F- 2F- 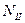 = 0
= 0
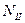 = - F (сжатие)
= - F (сжатие)
Проводим сечение с-с на участке III:
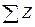 =
= 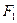 -
- 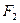 +
+ 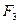 -
- 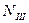 = 0
= 0
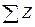 = F-2F + 4F-
= F-2F + 4F- 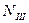 = 0
= 0
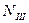 = 3F (растяжение)
= 3F (растяжение)
Строим эпюру.
Для построения эпюры N проводим ось абсцисс параллельно оси бруса.
Положительные значения откладываем вверх, отрицательные – вниз (рис. 4.1). Эпюра строится в выбранном м а с ш т а б е! Эпюру следует штриховать! Штриховка строго перпендикулярна оси эпюры!!! 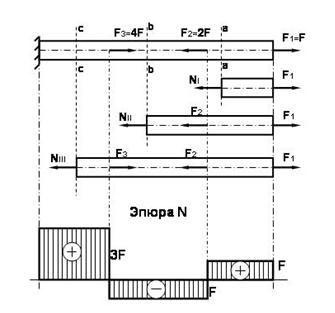
Рис. 4.1
Абсолютная и относительная продольная деформация.
Напряжение – это внутренняя сила, приходящаяся на единицу площади: 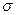 =
= 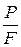 .
.
Единицы измерения напряжения:
1 Па = 1 Н/ м2; 1 МПа = 10 6 Па =1 Н/мм2.
Допускаемые напряжения ([ s ] и [ t ] – нормальные и касательные) – это такие максимальные напряжения, при которых не происходит разрушение данной конкретной детали, и она работает в условиях упругих деформаций.
При растяжении (сжатии) в поперечном сечении стержня 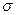 =
= 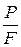 =
= 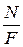 .
.
При растяжении нормальные напряжения – положительные, при сжатии – отрицательные.
Обратить внимание, что при растяжении- сжатии возникают только нормальные напряжения.
Изменение длины стержня 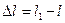 называют линейной продольной деформацией (абсолютным удлинением); изменение поперечного сечения
называют линейной продольной деформацией (абсолютным удлинением); изменение поперечного сечения 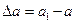 - линейной поперечной деформацией.
- линейной поперечной деформацией.
Интенсивность деформирования оценивают деформациями, приходящимися на единицу длинны стержня: относительной продольной 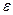 и относительной поперечной
и относительной поперечной 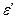 :
:
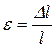 ;
; 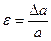 .
.
Деформации бывают продольные и поперечные. Отношение поперечной деформации к продольной называется коэффициентом Пуассона 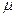 .
.
0,2 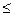
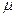
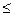 0,5.
0,5.
ЗАКОН ГУКА (открыт в 1660):
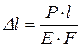 , (2)
, (2)
где 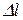 - абсолютная продольная деформация;
- абсолютная продольная деформация;
P – осевая внешняя сила;
F –площадь поперечного сечения;
E –модуль продольной упругости (модуль Юнга).
Закон Гука в форме (2) можно преобразовать, учитывая определения внутреннего напряжения (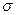 =
= 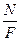 ) и относительной деформации (
) и относительной деформации (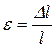 ):
):
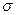 = E·
= E· 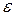 . (3)
. (3)
Максимальные напряжения при растяжении (сжатии): 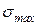 =
= 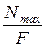 .
.
Тогда можно сформулировать условия прочности и жесткости при растяжении (сжатии).
Условие прочности: 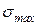
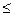
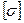 .
.
Условие жесткости: 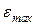
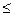
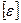 .
.
Условие жесткости при растяжении (сжатии) можно записать и в другом виде:
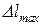 =
= 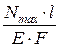
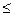
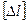 .
.
Изучить вопросы: закон Гука для абсолютных деформаций, закон Гука для нормальных напряжений.
Пример 2. Вычислить приращение длины стального стержня ступенчатого сечения, если 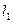 = 50 см,
= 50 см, 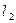 = 80 см,
= 80 см, 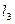 = 40 см,
= 40 см, 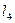 = 60 см, Е=2·
= 60 см, Е=2· 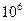
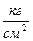 ,
, 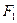 = 10
= 10 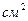 ,
, 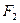 =20
=20 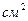 ,
, 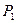 =200 кг,
=200 кг, 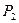 = 500 кг,
= 500 кг, 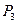 = 700 кг (рис. 1). Построить эпюры нормальных напряжений и перемещений.
= 700 кг (рис. 1). Построить эпюры нормальных напряжений и перемещений.
Решение
 2015-03-22
2015-03-22 2739
2739
