Для функции, значения которой приведены в таблице, Вычислить в узлах i=0,4 производную со вторым порядком точности по шагу h между узлами hi=xi.-xi-1. В одном из указанных узлов, где это возможно, провести уточнение значения производной с помощью метода Рунге-Ромберга.
| i | xi | yi |
| 1,0 | 1,302 | |
| 1,2 | 1,390 | |
| 1,4 | 1,551 | |
| 1,6 | 1,750 | |
| 1,8 | 1,610 |
1. Для вычисления производной в узлах i=0,4 будем использовать формулы численного дифференцирования второго порядка точности по шагу h (k=2) для крайних узлов:
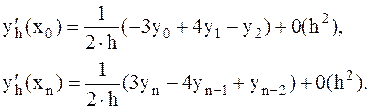
Имеем h=0,2. Получаем:
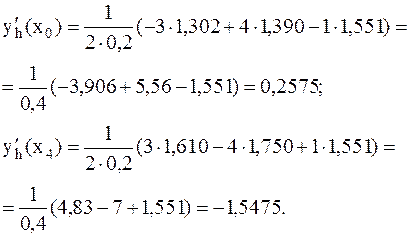
2. Для уточнения значения производной в заданном узле с помощью метода Рунге-Ромберга необходимо вычислить значение производной по той же формуле с шагом h1=p×h.
Полагаем p=2. Имеем h1=2h=2×0,2=0,4. Следовательно, для узла i=0 должны использоваться узлы: x0=1,0; x2=1,4 и x4=1,8; а в узле i=4 - узлы x4=1,8; x2=1,4 и x0=1,0. Так как значения функции в этих узлах известны, то можем провести вычисление с шагом h=0,4 в любом из них, например в узле i=4:
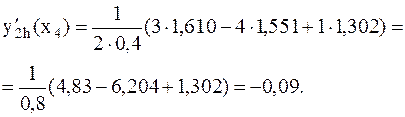
3. Для вычисления уточненного значения производной используем формулу Рунге-Ромберга при p=2 и k=2:
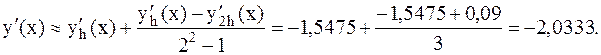
IV. Численное интегрирование.
1. Основные определения. Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при n®¥ и Dx®0:
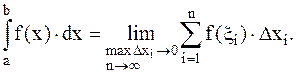 (4.1)
(4.1)
где, n-количество элементарных отрезков [xi-xi-1], i=1,...,n, на которые разбивается отрезок интегрирования [a,b], Dxi=(xi-xi-1)-длина i-ого отрезка, xi-точка на отрезке [xi-1,xi].
Когда функция f(x) задана аналитически в виде формулы и интеграл удается свести к табличному, то интеграл вычисляется с помощью таблиц неопределенных интегралов и формулы Ньютона-Лейбница, например:
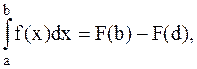 (4.2)
(4.2)
где F¢(x) - первообразная, т.е. F¢(x)=f(x).
Однако на практике обычно интегралы не сводятся известными приемами к табличным интегралам, даже тогда, когда под интегральная функция задана аналитически, не говоря уже о тех случаях, когда значения под интегральной f(x) заданы в виде таблицы. В этом случае используют численные методы.
2. Основные квадратурные формулы. Для вычисления определенных интегралов используется приближенное соотношение:
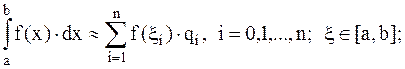 (4.2)
(4.2)
которое называется квадратурной формулой с узлами xi и весами gi.
В этой интеграл приближенно заменяется конечной суммой, члены которой представляют произведение значений функций в некоторых узлах на некоторую величину. Наиболее часто используются следующие квадратурные формулы (Рис.3):
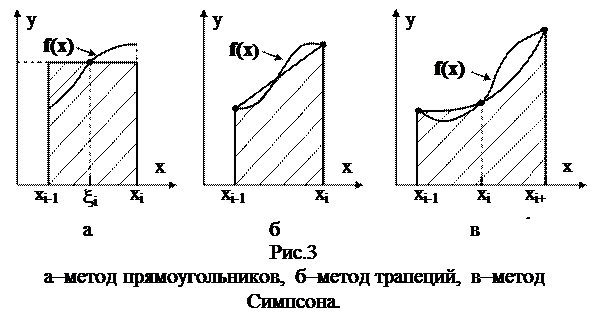 |
а) формула прямоугольников:
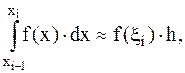 (4.3)
(4.3)
где 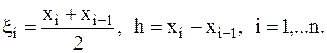 Для всего отрезка [a,b] имеем:
Для всего отрезка [a,b] имеем:
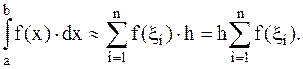 (4.4)
(4.4)
Погрешность формулы прямоугольников, полученная с помощью ряда Тейлора равна:
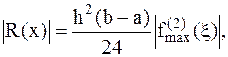 (4.5)
(4.5)
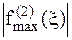 - максимальное значение второй производной на отрезке [a,b].
- максимальное значение второй производной на отрезке [a,b].
б) формула трапеции:
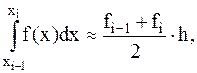 (4.6)
(4.6)
где fi=f(xi), i=1,...n. Для всего отрезка имеем:
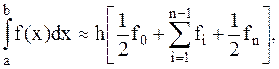 (4.7)
(4.7)
при этом погрешность равна:
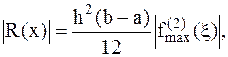 (4.8)
(4.8)
в) формула Симпсона (формула парабол):
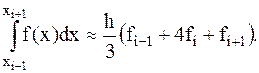 (4.9)
(4.9)
Для всего отрезка:
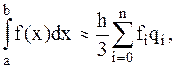 (4.10)
(4.10)
где
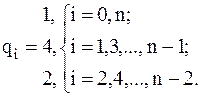 (4.11)
(4.11)
Погрешность формулы Симпсона равна:
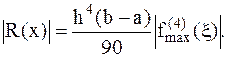 (4.12)
(4.12)
3. Правило Рунге практической оценки погрешности и уточнению по Ричардсону. Пусть I - точное значение интеграла, Ih - значение интеграла, вычисленное по квадратурной формуле с шагом h, а Ih/2- значение того же интеграла, вычисленное для шага h/2. Можем записать:
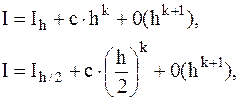 (4.13)
(4.13)
где c - константа.
Величина c×hk- называется главной частью погрешности квадратурной формулы с порядком точности k по шагу h. Остальная часть погрешности обозначена как 0(hk+1) и имеет порядок k+1.
Вычитая из первого уравнения второе, получаем соотношение, которое с точностью порядка 0(hk+1) позволяет вычислить значение главной части погрешности:
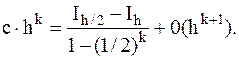 (4.14)
(4.14)
Данная формула называется практической оценкой погрешности по правилу Рунге, так как позволяет рассчитать абсолютную погрешность вычислений определенного интеграла с точностью до 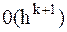 , т.е. можем записать:
, т.е. можем записать:
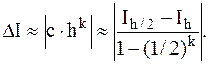 (4.15)
(4.15)
Подставляя выражение для главной части погрешности в первую формулу (4.13), получаем формулу для уточнения значение интеграла по Ричардсону:
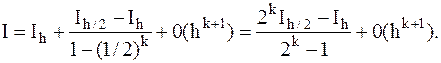 (4.16)
(4.16)
Для формул прямоугольников, трапеций и ячеек имеем k=2, для формул Симпсона-k=4.
Варианты задания №6.
Приближенно вычислить интеграл с использованием указанной в задании квадратурной формулы, при этом на всем отрезке интегрирования использовать пять узлов и в результате оставить только верные знаки. Методом Рунге оценить погрешность результата и методом Рунге-Ричардсона провести уточнение вычисленного значения интеграла
1. 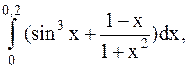 (метод трапеций).
(метод трапеций).
2. 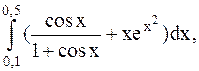 (метод Симпсона).
(метод Симпсона).
3. 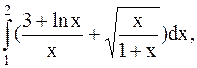 (метод Симпсона).
(метод Симпсона).
4. 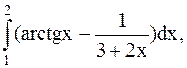 (метод трапеций).
(метод трапеций).
5. 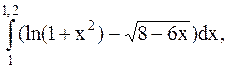 (метод Симпсона).
(метод Симпсона).
6. 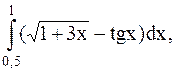 (метод прямоугольников).
(метод прямоугольников).
7. 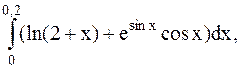 (метод Симпсона).
(метод Симпсона).
8. 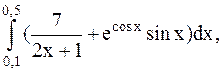 (метод трапеций).
(метод трапеций).
9. 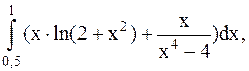 (метод Симпсона).
(метод Симпсона).
10. 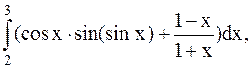 (метод Симпсона).
(метод Симпсона).
11. 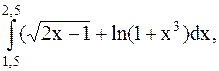 (метод трапеций).
(метод трапеций).
12. 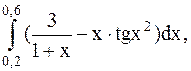 (метод трапеций).
(метод трапеций).
13. 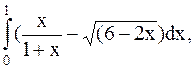 (метод прямоугольников).
(метод прямоугольников).
14. 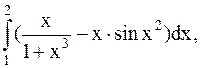 (метод Симпсона).
(метод Симпсона).
15. 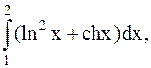 (метод трапеций).
(метод трапеций).
16. 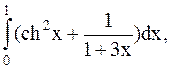 (метод прямоугольников).
(метод прямоугольников).
17. 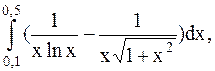 (метод Симпсона).
(метод Симпсона).
18. 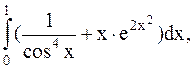 (метод Симпсона).
(метод Симпсона).
19. 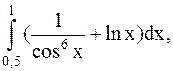 (метод трапеций).
(метод трапеций).
20 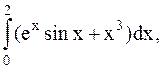 (метод трапеций).
(метод трапеций).
21. 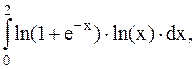 (метод прямоугольников)
(метод прямоугольников)
22. 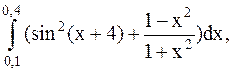 (метод трапеций).
(метод трапеций).
23. 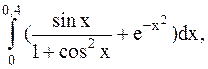 (метод Симпсона).
(метод Симпсона).
24. 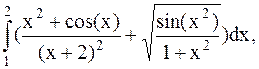 (метод Симпсона).
(метод Симпсона).
25. 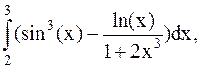 (метод трапеций).
(метод трапеций).
26. 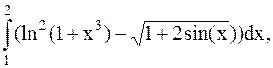 (метод Симпсона).
(метод Симпсона).
27. 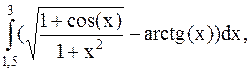 (метод прямоугольников).
(метод прямоугольников).
28. 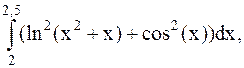 (метод Симпсона).
(метод Симпсона).
29. 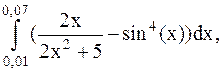 (метод трапеций).
(метод трапеций).
30. 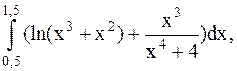 (метод Симпсона).
(метод Симпсона).
31. 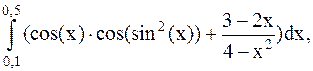 (метод Симпсона).
(метод Симпсона).
32. 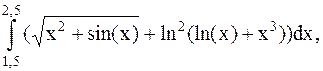 (метод трапеций).
(метод трапеций).
33. 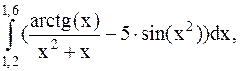 (метод трапеций).
(метод трапеций).
34. 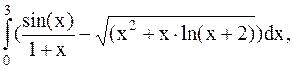 (метод прямоугольников).
(метод прямоугольников).
35. 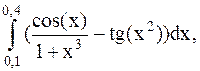 (метод Симпсона).
(метод Симпсона).
36. 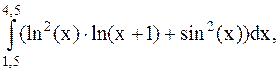 (метод трапеций).
(метод трапеций).
37. 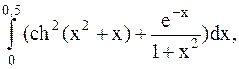 (метод прямоугольников).
(метод прямоугольников).
38. 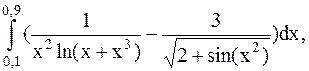 (метод Симпсона).
(метод Симпсона).
39. 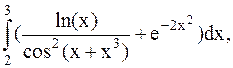 (метод Симпсона).
(метод Симпсона).
40. 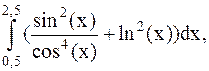 (метод трапеций).
(метод трапеций).
 2015-03-22
2015-03-22 6061
6061
