III. Численное дифференцирование

1. Аппроксимация производных конечными разностями. Производной функции y=f(x) называется предел:

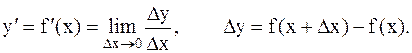(3.1)

Для приближенного вычисления производной используется формула:

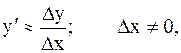(3.2)

где Dx-некоторое конечное число. Данное соотношение называют аппроксимацией производной с помощью конечных разностей, т.к. величина Dx конечна и не равна нулю.

Пусть известны значения функции y₀,y₁,...,y_i,...,y_n, вычисленные или заданные таблицей, в точках x₀,x₁,...,x_i,...,x_n (Рис.2). Точки x₀,x₁,...,x_i,...,x_n называются узлами, а разность между соседними значениями аргумента называется шагом h_i=Dx_i=x_i-x_i-1, i=1,...,n. Весь набор узлов называется сеткой. Если величина шага между узлами постоянна, то говорят, что узлы x₀,x₁,...,x_i,...,x_n образуют равномерную сетку с шагом h.

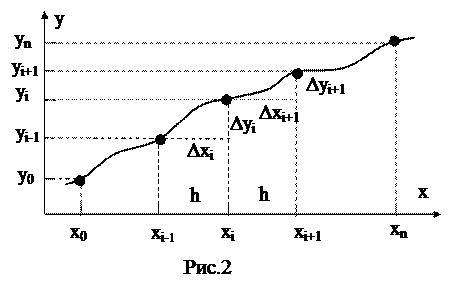Для вычисления производной y¢_i в точке точки x_i по формуле можно использовать различные разности, например, левую разность,

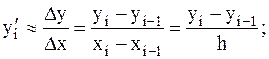(3.3)

правую разность:

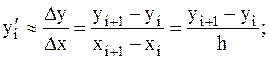(3.4)

центральную разность:

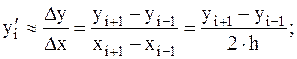(3.5)

и т.п.

2. Погрешность численного дифференцирования. При численном дифференцировании с использованием приближенной формулы, использующей конечно-разностное соотношение, естественно возникает погрешность: R(x,h)=y¢(x)-y¢_h(x,h), где y¢(x)-точное значение производной, а y¢_h(x,h)- значение производной вычисленное по приближенной формуле при шаге h.

Величина погрешности зависит от точки x, в которой вычисляется производная, и от шага h. При этом, чем меньше шаг, тем меньше погрешность. Обычно погрешность R(x,h) записывают одним из способов:

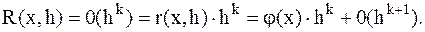(3.6)

где, j(x)×h^k- называется главной частью погрешности аппроксимации, т.к. это слагаемое при h<<1 будет гораздо больше второго, а величина k называется порядком погрешности или порядком точности аппроксимации относительно шага h.

3. Аппроксимирующие формулы первого, второго и четвертого порядка точности. Аппроксимацию производных конечными разностями в общем случае можно рассматривать как замену производной от функции y¢=f¢(x) производной от аппроксимирующей функции j¢(x), j(x)»f(x), где в качестве аппроксимирующей функции используется интерполяционный многочлен:

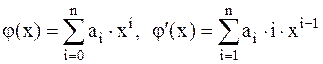. (3.7)

Так как точность аппроксимации определяется степенью интерполяционного многочлена, то увеличивая степень многочлена n мы будем увеличивать и порядок точности аппроксимации производной.

С помощью интерполяционного многочлена Лагранжа при равномерном распределении узлов были получены следующие формулы первого порядка точности для аппроксимации производной с помощью левой и правой разности:

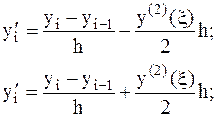(3.8)

а также второго и четвертого порядка точности с помощью центральных разностей:

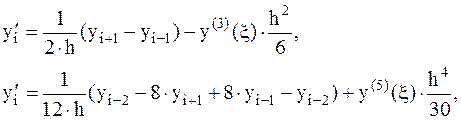(3.9)

где, y^(k)(x) - значение “к”-той производной в некоторой точке на отрезке, которому принадлежат используемые в формуле узлы.

В крайних точках таблицы или в крайних узлах нельзя использовать соотношения для центральных разностей, которые имеют порядок точности два и выше. Поэтому в этих точках используются следующие односторонние формулы численного дифференцирования второго порядка точности:

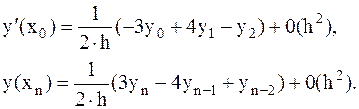(3.10)

4. Улучшение аппроксимации с помощью метода Рунге -Ромберга. Пусть y¢(x) - точное значение производной, а y¢_h(x) -значение производной, вычисляемое по формуле численного дифференцирования, имеющей порядок точности к относительно шага h. Следовательно, можем записать:

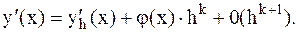(3.11)

Запишем это же соотношение для шага h₁=ph:

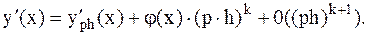
Вычитая из второго соотношения первое получаем формулу для главной части погрешности, имеющей точность на порядок выше, чем порядок точности используемой формулы численного дифференцирования:

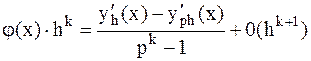. (3.12)

Подставляя эту формулу в исходную формулу, получаем:

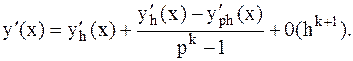(3.13)

Данное соотношение позволяет по результатам двух расчетов производной с шагом h и шагом ph с использованием одной и той же формулы численного дифференцирования, имеющей порядок точности k, найти уточненное значение производной с порядком точности k+1. Данный прием называется методом Рунге-Ромберга.

Варианты задания №5.

Для функции, значения которой приведены в таблице, вычислить в указанных узлах производную со вторым порядком точности по шагу h между узлами h_i=x_i.-x_i-1. В одном из указанных узлов, где это возможно, провести уточнение значения производной с помощью метода Рунге-Ромберга.

1. i=1,2,3;

i	xi	yi
	1,0	1,302
	1,2	1,390
	1,4	1,551
	1,6	1,750
	1,8	2,105

2. i=0,4;

i	xi	yi
	0,2	0,402
	0,6	1,490
	1,0	2,681
	1,4	4,000
	1,8	5,340

3. i=1,2,3;

i	xi	yi
	0,1	0,430
	0,2	0,390
	0,3	0,281
	0,4	0,175
	0,5	0,085

4. i=0,4;

i	xi	yi
	1,2	0,502
	1,6	0,904
	2,0	1,871
	2,4	1,478
	2,8	0,443

5. i=1,2,3;

I	xi	yi
	0,0	10,50
	1,0	12,72
	2,0	12,55
	3,0	11,07
	4,0	10,05

6. i=0,4;

i	xi	yi
	0,02	0,002
	0,04	0,640
	0,06	0,647
	0,08	0,597
	0,10	0,130

7. i=1,2,3;

i	xi	yi
	1,0	4,397
	1,5	1,740
	2,0	-1,551
	2,5	-2,450
	3,0	-2,075

8. i=0,4;

i	xi	yi
	0,1	0,542
	0,2	0,990
	0,3	0,942
	0,4	0,440
	0,5	-0,530

9.i=1,2,3;

i	xi	yi
	0,00	0,722
	0,25	0,905
	0,50	0,551
	0,75	0,048
	1,00	-0,805

10. i=0,4;

i	xi	yi
	0,0	-0,039
	0,1	-1,370
	0,2	-0,759
	0,3	0,446
	0,4	5,450

11. i=1,2,3;

i	xi	yi
	1,2	41,02
	1,4	52,90
	1,6	31,51
	1,8	11,750
	2,0	-0,105

12. i=0,4;

i	xi	yi
	1,0	4,035
	1,5	3,068
	2,0	2,081
	2,5	4,564
	3,0	4,560

13. i=1,2,3;

i	xi	yi
	0,0	0,022
	0,3	0,906
	0,6	0,555
	0,9	0,350
	1,2	-0,205

14 i=0,4;

i	xi	yi
	0,2	0,0290
	0,4	0,0875
	0,6	0,0653
	0,8	-0,2222
	1,0	5,340

15.i=1,2,3;

i	xi	yi
	0,01	0,0202
	0,02	0,0320
	0,03	0,055
	0,04	0,075
	0,05	0,155

16.i=0,4;

i	xi	yi
	0,01	0,0072
	0,02	0,0470
	0,03	0,0958
	0,04	0,0539
	0,05	0,0480

17. i=1,2,3;

i	xi	yi
	0,4	5,802
	0,8	6,360
	1,2	7,541
	1,6	8,760
	2,0	8,135

18. i=0,4;

i	xi	yi
	10,0	5,889
	11,0	3,335
	12,0	3,773
	13,0	6,587
	14,0	8,863

19. i=1,2,3;

i	xi	yi
	1,0	17,02
	2,0	13,90
	3,0	12,34
	4,0	13,50
	5,0	21,18

20. i=0,4;

i	xi	yi
	0,00	0,993
	0,25	0,774
	0,50	0,439
	0,75	0,485
	1,00	0,695

21. i=1,2,3;

i	xi	yi
	2,0	-8,302
	2,2	1,450
	2,4	-6,720
	2,6	3,921
	2,8	3,706

22. i=0,4;

i	xi	yi
	0,3	3,734
	0,6	4,120
	0,9	5,123
	1,2	-3,850
	1,5	-6,220

23. i=1,2,3;

i	xi	yi
	0,5	-0,430
	1,5	0,390
	2,5	0,564
	3,5	0,755
	4,5	0,893

24. i=0,4;

i	xi	yi
	1,2	-5,902
	1,6	-8,320
	2,0	-10,450
	2,4	-14,540
	2,8	-16,519

25. i=1,2,3;

I	xi	yi
	0,8	0,650
	1,6	1,790
	2,4	2,745
	3,2	3,333
	4,0	5,309

26. i=0,4;

i	xi	yi
	0,02	0,598
	0,04	0,760
	0,06
	0,08	0,977
	0,10	1,345

27. i=1,2,3;

i	xi	yi
	-1,0	7,540
	-1,5	7,321
	-2,0	6,644
	-2,5	4,130
	-3,0	-3,022

28. i=0,4;

i	xi	yi
	-0,1	3,380
	-0,2	4,550
	-0,3	5,640
	-0,4	6,440
	-0,5	7,220

29.i=1,2,3;

i	xi	yi
		-0,722
		-0,880
		-0,340
		0,048
		0,455

30. i=0,4;

i	xi	yi
	0,0	4,427
	0,1	5,870
	0,2	6,760
	0,3	8,330
	0,4	9,990

31. i=1,2,3;

i	xi	yi
	-1,2	4,020
	-1,4	-5,900
	-1,6	3,510
	-1,8	-1,750
	-2,0	-2,105

32. i=0,4;

i	xi	yi
	-1,0	1,122
	-1,5	3,330
	-2,0	4,280
	-2,5	5,650
	-3,0	6,750

33. i=1,2,3;

i	xi	yi
		-0,554
		-0,665
		-0,734
		-0,980
		-1,140

34 i=0,4;

i	xi	yi
	-0,2	-290
	-0,4
	-0,6
	-0,8
	-1,0

35.i=1,2,3;

i	xi	yi
	-0,01	-2,360
	-0,02	3,707
	-0,03	5,540
	-0,04	6,430
	-0,05	8,908

36. i=0,4;

i	xi	yi
	0,06	-0,56
	0,12	-0,450
	0,18	-0,330
	0,24	-0,220
	0,30	-0,140

37. i=1,2,3;

i	xi	yi
	-0,4	8,02
	-0,8	3,60
	-1,2	5,41
	-1,6	7,60
	-2,0	8,80

38.i=0,4;

i	xi	yi
	16,0	-8,120
	31,0	-2,870
	46,0	-3,540
	61,0	-4,890
	76,0	-6,555

39.i=1,2,3;

i	xi	yi
	-1,0	7,50
	-2,0	23,66
	-3,0	52,88
	-4,0	73,51
	-5,0	91,57

40.i=0,4;

i	xi	yi
	0,00
	-0,25
	-0,50
	-0,75
	-1,00