Конечные разности различных порядков

Пусть 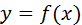- заданная функция. Обозначим через 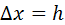фиксированную величину приращения аргумента (шаг). Тогда выражение

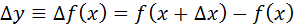(1)

называется первой конечной разностью функции y. Аналогично определяются конечные разности высших порядков

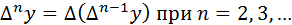
Например

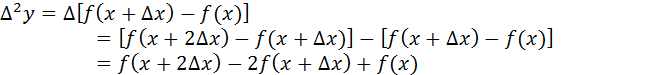
Справедиливо утверждение:

если 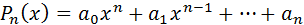– полином n -й степени, то 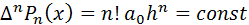, где .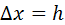

Следствие: 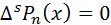при .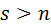

Символ (дельта) можно рассматривать как оператор, ставящий в соответствие функции 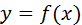функцию 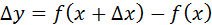( 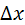постоянно).

По определению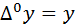

Из формулы (1) имеем:

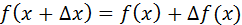
отсюда, рассматривая как символический множитель, получим:

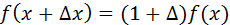(2)

Последовательно применяя это соотношение n раз, будем иметь:

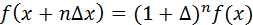(3)

Воспользовавшись формулой бинома Ньютона, окончательно выводим:

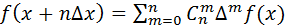(4)

где 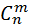- число сочетаний из n элементов по m.

Таким образом, с помощью формулы (4) последовательные значения функции 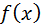выражаются через ее конечные разности различных порядков.

Воспользовавшись тождеством 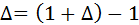(5) и применяя бином Ньютона и формулу (3), получаем:

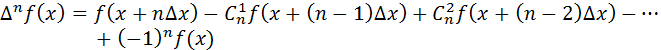
Эта формула дает выражение конечной разности n -го порядка функции 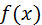через последовательные значения этой функции.

Пусть функция 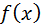имеет непрерывную производную 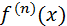на отрезке 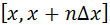. Тогда справедлива формула 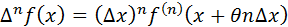, где 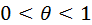. Тогда при малых 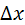справедлива приближенная формула .

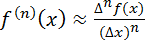Таблица разностей

Часто приходится рассматривать функции 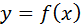, заданные табличными значениями 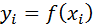для системы равноотстоящих точек 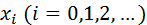, где .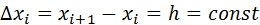

Использовав формулу бинома Ньютона, получим:

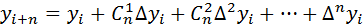
Обратно имеем:

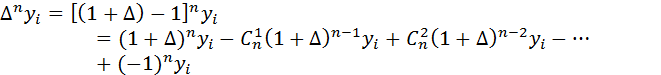
или

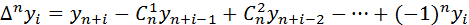
Например, ,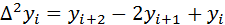

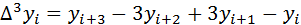
Заметим, что для вычисления n -й разности 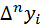нужно знать n+1 членов 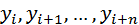данной последовательности.

Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной таблицы разностей или диагональной таблицы разностей (рисунок 1, 2).