Первая интерполяционная формула Ньютона

Пусть для функции 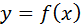заданы значения 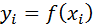для равноотстоящих значений независимой переменной: 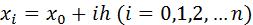, где h – шаг интерполяции. Требуется подобрать полином 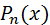степени не выше n, принимающий в точках 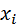значения
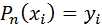
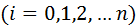(1)

Условия (1) эквиваленты тому, что 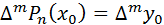при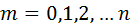

Пользуясь обобщенной степенью, выражение (1) может быть записано следующим образом:

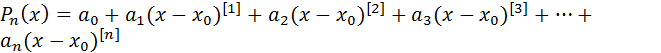(2)

Коэффициенты 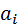можно рассчитать по формуле 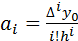где 0!=1 и 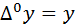, тогда подставляя значения коэффициентов 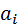в выражение (2) получим интерполяционный полином Ньютона

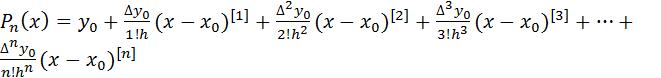(3)

Полином (3) полностью удовлетворяет требованиям поставленной задачи. Заметим, что при 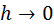формула (3) превращается в полином Тейлора для функции y.

Для практического использования интерполяционную формулу (3) обычно записывают в преобразованном виде используя вспомогательную переменную 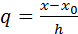, тогда выражение (3) принимает следующий вид 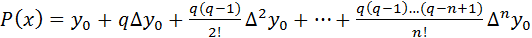, (4)
где 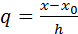представляет собой число шагов, необходимых для достижения точки 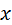, исходя из точки 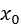. Это и есть окончательный вид первой интерполяционной формулы Ньютона.

Заметим, что если таблица значений функции конечна, то число n ограничено, а именно: n не может быть больше числа значений функции y, уменьшенного на единицу.