При большом числе неизвестных линейной системы схема метода Гаусса, дающая точное решение, становится весьма сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться приближенными численными методами.
Пусть дана линейная система
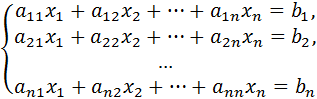 (1)
(1)
Введем в рассмотрение матрицы
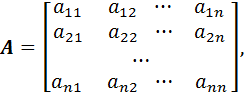
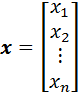 ,
, 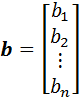 .
.
Тогда систему (1) коротко можно записать в виде матричного уравнения
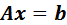 (1’)
(1’)
Предполагая, что диагональные коэффициенты 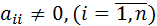 ,
,
Решим первое уравнение системы (1) относительно 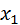 , второе – относительно
, второе – относительно 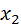 и т.д. Тогда получим эквивалентную систему:
и т.д. Тогда получим эквивалентную систему:
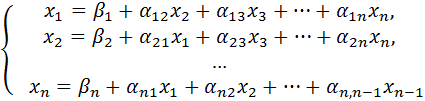 (2)
(2)
где 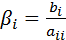 ;
; 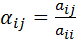 при
при 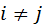 и
и 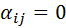 при
при 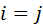
Введем матрицы
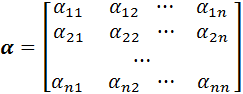 и
и 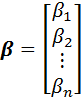 ,
,
тогда систему (2) можно записать в матричной форме
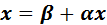 (2’)
(2’)
Систему (2) решим методом последовательных приближений. За нулевое приближение примем столбец свободных членов 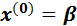 .
.
Далее, последовательно строим матрицы-столбцы
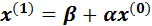 (первое приближение)
(первое приближение)
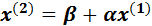 (второе приближение)
(второе приближение)
и т.д.
В общем случае, любое 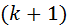 -е приближение вычисляют по формуле
-е приближение вычисляют по формуле
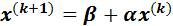 (
(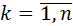 ). (3)
). (3)
Если последовательность приближений 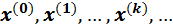 имеет предел
имеет предел 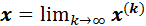 , то этот предел является решением системы (2). Действительно, переходя к пределу в равенстве (3) будем иметь:
, то этот предел является решением системы (2). Действительно, переходя к пределу в равенстве (3) будем иметь:
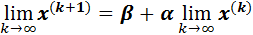
или
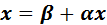
т.е. предельный вектор 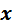 являетсярешением системы (2’), а, следовательно, и системы (1).
являетсярешением системы (2’), а, следовательно, и системы (1).
Напишем формулы приближений в развернутом виде:
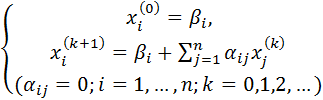 (3’)
(3’)
Заметим, что иногда выгоднее приводить систему (1) к виду (2) так, чтобы коэффициенты 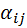 не были равны нулю.
не были равны нулю.
Вообще, имея систему
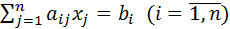 ,
,
можно положить:
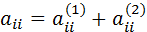 ,
,
где 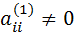 . Тогда данная система эквивалентна приведенной системе
. Тогда данная система эквивалентна приведенной системе
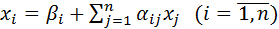 ,
,
где
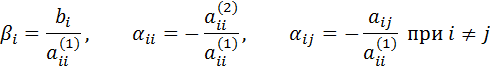
Поэтому в дальнейшем будем предполагать 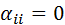 .
.
Метод последовательных приближений, определяемых формулой (3) или (3’), носит название метода итерации. Процесс итерации (3) хорошо сходится, т.е. число приближений, необходимых для получения корней системы (1) с заданной точностью, невелико, если элементы матрицы 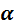 малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы (1) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют).
малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы (1) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют).
Замечание: При применении метода итерации (формула (3)) нет необходимости за нулевое приближение 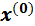 принимать столбец свободных членов. Сходимость процесса итерации зависит только от свойств матрицы
принимать столбец свободных членов. Сходимость процесса итерации зависит только от свойств матрицы 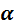 , причем при выполнении известных условий, если этот процесс сходится при каком-нибудь выборе исходного начального приближения, то он будет сходиться к тому же предельному вектору и при любом другом выборе этого начального приближения. Поэтому начальный вектор
, причем при выполнении известных условий, если этот процесс сходится при каком-нибудь выборе исходного начального приближения, то он будет сходиться к тому же предельному вектору и при любом другом выборе этого начального приближения. Поэтому начальный вектор 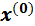 в процессе итерации может быть взят произвольным. Целесообразно за компоненты начального вектора выбирать приближенные значения корней системы, находимые грубой прикидкой.
в процессе итерации может быть взят произвольным. Целесообразно за компоненты начального вектора выбирать приближенные значения корней системы, находимые грубой прикидкой.
Сходящийся процесс итерации обладает важным свойством самоисправляемости, т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, так как ошибочное приближение можно рассматривать как новый начальный вектор.
Отметим, что иногда бывает удобнее подсчитывать не сами приближения, а их разности.
Недостатком этого варианта метода итерации является систематическое накопление ошибок при увеличении числа слагаемых, в результате чего могут возникнуть значительные погрешности искомых корней. Кроме того, ошибка, допущенная в вычислениях, повлияет на окончательный результат. Поэтому надежнее пользоваться первым вариантом метода итерации.
Замечания о точности расчета. Если все коэффициенты и свободные члены данной системы являются точными числами, то решение ее методом последовательных приближений может быть получено с любым заранее заданным числом m верных десятичных знаков. При этом в значениях последовательных приближений следует удерживать m+1 десятичных знаков и последовательные приближения вычислять до их совпадения, после чего нужно округлить результат на один знак. Если коэффициенты и свободные члены данной системы являются приближенными числами, написанными с p знаками, то решение этой системы производится, как в случае точных чисел, с точностью до m=p знаков.
Рассмотрим без доказательства достаточное условие сходимости процесса итерации.
Теорема. Если для приведенной системы (2) выполнено по меньшей мере одно из условий
1) 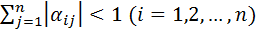
или
2) 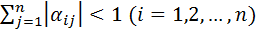 , то процесс итерации (3) сходится к единственному решению этой системы, независимо от выбора начального приближения.
, то процесс итерации (3) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Следствие: Для системы 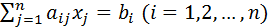 метод итерации сходится, если выполнены неравенства
метод итерации сходится, если выполнены неравенства 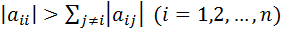 , т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
, т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
 2015-03-22
2015-03-22 1264
1264
