При решении практических задач часто нужно найти производные указанных порядков от функции 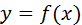 , заданной таблично. Возможно также, что в силу сложности аналитического выражения функции
, заданной таблично. Возможно также, что в силу сложности аналитического выражения функции 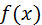 непосредственное дифференцирование затруднительно. В этих случаях обычно прибегают к приближенному дифференцированию.
непосредственное дифференцирование затруднительно. В этих случаях обычно прибегают к приближенному дифференцированию.
Для вывода формул приближенного дифференцирования заменяют данную функцию 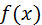 на интересующем отрезке
на интересующем отрезке 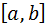 интерполирующей функцией
интерполирующей функцией 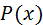 (чаще всего полиномом), а затем полагают:
(чаще всего полиномом), а затем полагают:
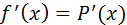 при
при 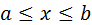 (1)
(1)
Аналогично поступают при нахождении производных высших порядков функции 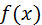 .
.
Если для интерполирующей функции 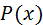 известна погрешность
известна погрешность 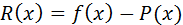 , то погрешность производной
, то погрешность производной 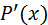 выражается формулой
выражается формулой
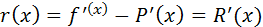 , (2)
, (2)
т.е. погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же самое справедливо и для производных высших порядков.
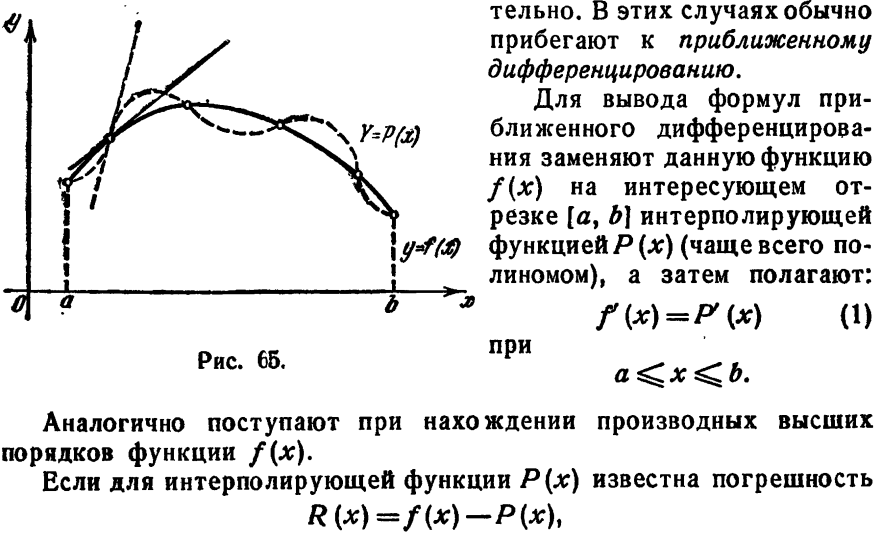
Приближенное дифференцирование представляет собой операцию менее точную, чем интерполирование. Действительно, близость друг к другу ординат двух кривых 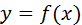 и
и 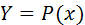 на отрезке
на отрезке 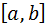 еще не гарантирует близости на этом отрезке их производных
еще не гарантирует близости на этом отрезке их производных 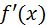 и
и 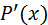 , т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента (рис. 1).
, т.е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента (рис. 1).
Формулы приближенного дифференцирования,
основанные на первой интерполяционной формуле Ньютона
Пусть имеем функцию, заданную в равноотстоящиъ точках отрезка с помощью значения. Для нахождения на производных функцию приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов

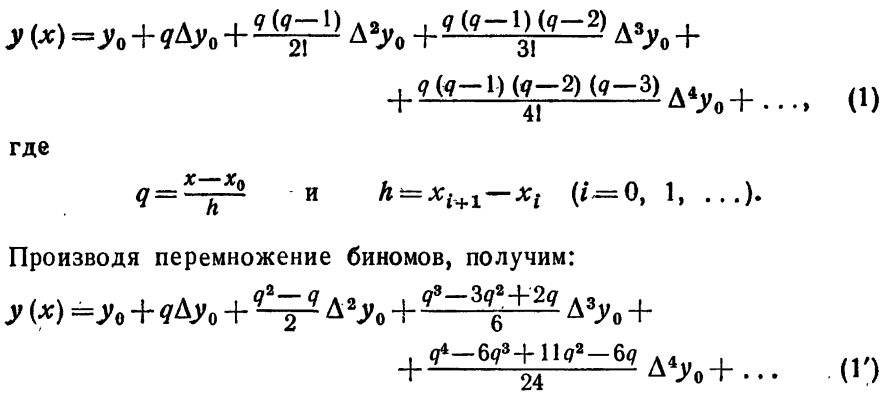
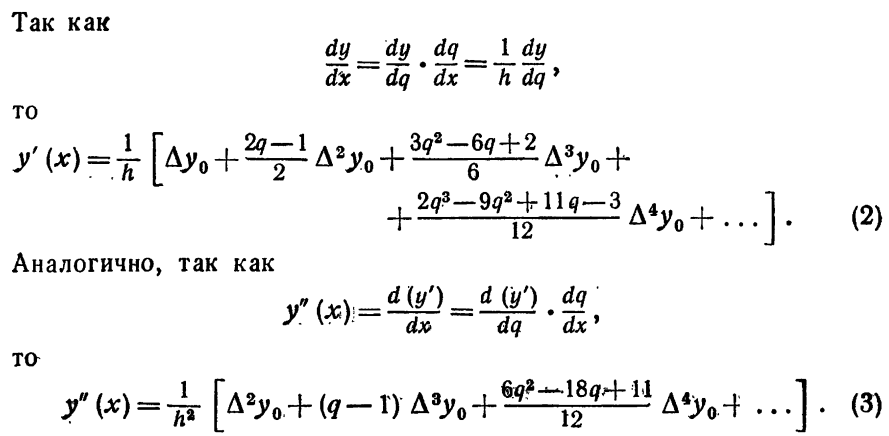











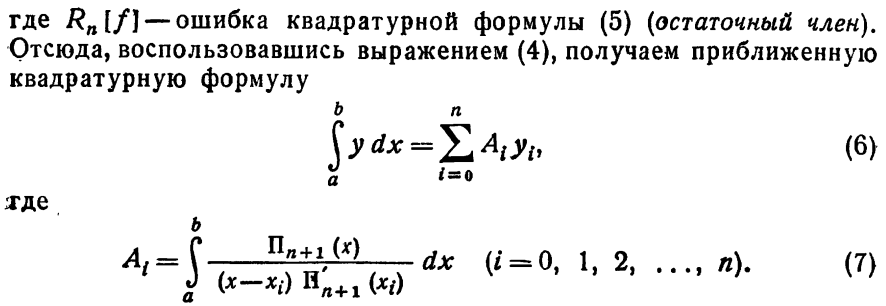


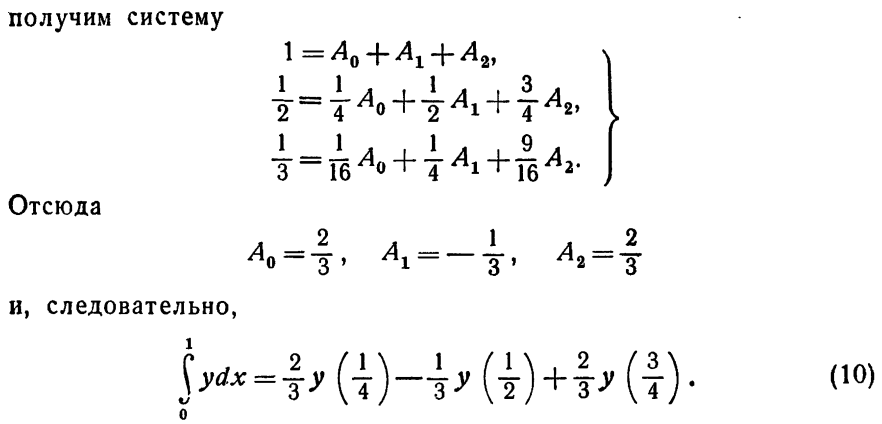



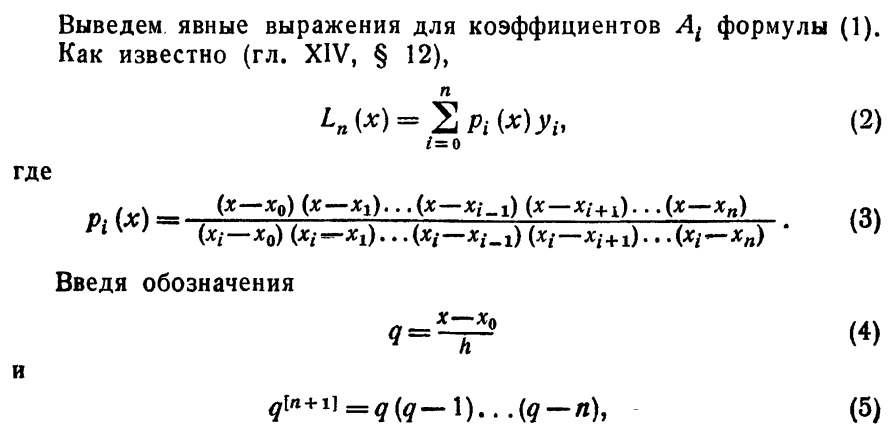


 2015-03-22
2015-03-22 646
646







