Уравнение Лагранжа

Уравнением вида (4), для которого интегрирование уравнения (6) всегда возможно, является уравнение Лагранжа.

Определение. Уравнение вида

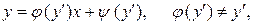(12)

в котором 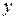является линейной функцией от 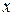с коэффициентом, зависящим от 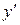, причем коэффициент при 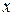не равен 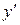, называется уравнением Лагранжа.

Решение уравнения. Уравнение (12) относится к уравнениям вида (4), поэтому для его интегрирования надо воспользоваться методом введения параметра. Обозначим 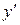через 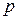. Тогда уравнение перепишется в виде

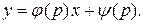(13)

Дифференцируя его по 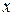, получим

.

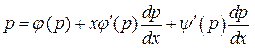Если в этом уравнении рассматривать переменную 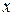как искомую функцию, а 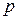как независимое переменное, получим линейное уравнение

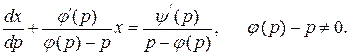(14)

Известно, что это уравнение интегрируется в квадратурах. Отсюда следует, что и уравнение Лагранжа будет уравнением, интегрируемым в квадратурах.

Пусть

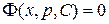(15)

– общий интеграл уравнения (14).

1) Если равенство (15) разрешимо относительно 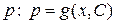, то, под-

ставляя эту функцию в (13), получим общее решение уравнения Лагранжа

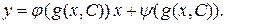
2) Если равенство (15) разрешимо относительно 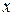: 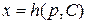, то, под-

ставляя выражение для 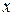в (13), получим 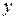как функцию от :

.

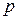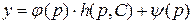В данном случае решение уравнения Лагранжа записывается в параметрическом виде: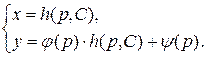

Замечание. Если уравнение 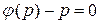имеет действительные решения 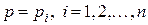, то, подставляя их в уравнение (13) и, принимая во внимание, что 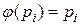, получаем

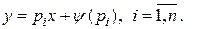
– частные решения уравнения Лагранжа, не входящие в общее решение. Эти решения могут оказаться особыми решениями уравнения Лагранжа.