Особые решения

В настоящем параграфе исследуется вопрос о существовании особых решений уравнений первого порядка и указываются способы их нахождения.

Определение. Особым решением дифференциального уравнения называется такое его решение, в каждой точке которого нарушается единственность

решения задачи Коши.

Свойство единственности решения, удовлетворяющего условию 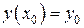, обычно понимается в том смысле, что через данную точку 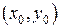проходит не более одной интегральной кривой уравнения по данному направлению.

Заметим, что если через точку 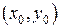проходит две интегральные кривые уравнения 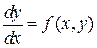, то в этой точке они касаются или, иначе, проходят через точку по одному направлению, так как угловой коэффициент касательной к интегральным кривым в точке 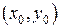равный 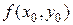определяется однозначно. В этом случае нарушается свойство единственности решения.

Для уравнения вида 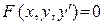через некоторую точку, вообще говоря, может проходить не одна, а несколько интегральных кривых каждая со своей касательной (см. пр. 10). Поэтому для таких уравнений тот факт, что через точку 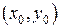проходит более одной интегральной кривой еще не означает нарушения свойства единственности решения. Это свойство нарушается, если через точку проходит более одной интегральной кривой по одному и тому же направлению.

Итак, геометрически особому решению соответствует такая интегральная кривая, через каждую точку которой, кроме нее самой, по тому же направлению проходит еще, по крайней мере, одна интегральная кривая уравнения.

6.1 Нахождение особого решения уравнения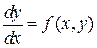

Если в области 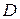, в которой рассматривается уравнение

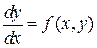(1)

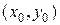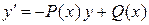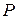соблюдаются условия теоремы Коши существования и единственности решения, то через каждую точку этой области проходит единственная интегральная кривая. Очевидно, особых решений в такой области уравнение не имеет. Например, линейное уравнение , где и 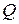непрерывные функции на отрезке 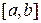, не имеет особых решений в полосе 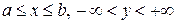, так как в этой области выполняются условия теоремы Коши. Итак, теорема Коши дает достаточные условия для того, чтобы в некоторой области не существовало особых решений. Следовательно, для существования особого решения необходимо, чтобы в этой области не выполнялись условия теоремы Коши. Заметим, что, так как теорема Коши дает только достаточные условия единственности решения, то не выполнение этих условий дает только необходимые условия существования особого решения.

Из всего сказанного следует, что для нахождения особого решения уравнения (1) надо поступить следующим образом.

1) Найти геометрическое место точек, где не выполняются условия теоремы Коши. В частности, если функция 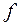непрерывна (что обычно выполнено), надо найти геометрическое место точек, в которых производная 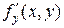не является непрерывной. Пусть это геометрическое место точек образует одну или несколько кривых.

2) Проверить являются ли эти кривые интегральными кривыми уравнения; если они не являются интегральными кривыми, то делаем вывод, что уравнение не имеет особых решений; если какая - нибудь из кривых является интегральной кривой, то переходим к следующему пункту.

3)Для отобранных решений проверить выполнение определения особого решения.

Для того чтобы интегральная кривая 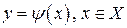была особой, то есть в каждой своей точке она пересекалась с некоторой кривой из семейства интегральных кривых 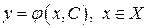, требуется, чтобы выполнялось условие пересечения

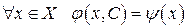. (2)

Если для каждого 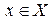существует хотя бы одно решение 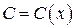этого уравнения, то решение 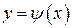является особым решением уравнения (1).

Поясним сказанное на примерах.

Пример 16. Выяснить имеют ли особые решения уравнения:

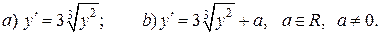
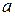▲ ) В данном случае .

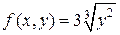1) Находим геометрическое место точек, в которых нарушаются условия

теоремы Коши существования и единственности решения. Функция 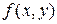является непрерывной функцией на 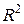. Производная 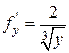непрерывна на 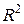, за исключением точек 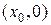, принадлежащих линии 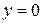. Следовательно, 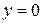может быть особым решением уравнения.

2) Непосредственной подстановкой в уравнение, убеждаемся, что 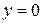есть решение данного уравнения.

3) Найдем общее решение уравнения:

.

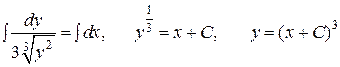Запишем условие (2) пересечения интегральной кривой 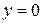с интегральными кривыми семейства 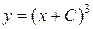: 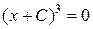. Для любого 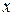существует решение этого уравнения: 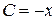. Следовательно, 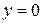является особым решением данного дифференциального уравнения (рис.10).

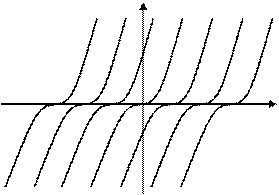Рис. 10

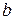) Имеем 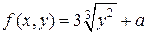. Функция 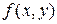непрерывна на всей плоскости, а ее производная 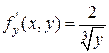не определена в точках оси 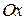. Поэтому линия 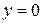может быть особым решением уравнения. Непосредственной подстановкой в уравнение убеждаемся, что 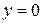не является решением. Следовательно, уравнение особых решений не имеет. ▲