Однако, не всегда уравнение (1) можно разрешить относительно производной, таковы, например, уравнения 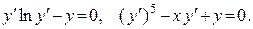 В некоторых случаях к уравнениям вида (1) применим своеобразный метод решения, который называется методом введения параметра. Этот метод применяется, если уравнение (1) легко разрешается относительно переменной
В некоторых случаях к уравнениям вида (1) применим своеобразный метод решения, который называется методом введения параметра. Этот метод применяется, если уравнение (1) легко разрешается относительно переменной 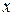 или
или 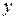 , то есть оно представимо в виде
, то есть оно представимо в виде 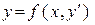 или
или 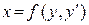
Рассмотрим уравнение вида
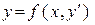 (4)
(4)
которое является уравнением, неразрешенным относительно производной, но разрешенным относительно искомой функции.
Решение уравнения. Данное уравнение интегрируется методом введения параметра. Обозначим 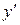 через
через 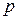 . Тогда, подставляя
. Тогда, подставляя 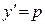 в (4), получим
в (4), получим
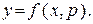 (5)
(5)
Дифференцируем (5) по 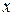 , учитывая, что
, учитывая, что 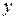 зависит от
зависит от 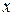 как непосредствен-
как непосредствен-
но, так и через промежуточную переменную 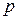 :
:
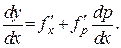
Заменяем 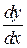 через
через 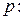
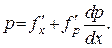
Разрешая это уравнение относительно 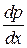 , получим уравнение
, получим уравнение
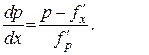 (6)
(6)
Дифференциальное уравнение (6) является уже уравнением, разрешенным относительно производной. Предположим, что уравнение (6) интегрируется в квадратурах и его общий интеграл есть
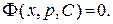 (7)
(7)
Могут представиться два случая:
1) равенство (7) разрешимо относительно 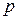 , то есть
, то есть 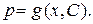 Тогда, подставляя выражение для
Тогда, подставляя выражение для 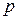 в (5), получим общее решение уравнения (4) в явном виде
в (5), получим общее решение уравнения (4) в явном виде
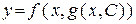 ; (8)
; (8)
2) равенство (7) разрешимо относительно 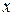 , то есть
, то есть 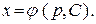 Подставляя значение
Подставляя значение 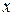 в (5), получим
в (5), получим 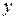 как функцию параметра
как функцию параметра 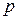 :
:
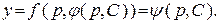 (9)
(9)
В итоге получим общее решение уравнения (4) в параметрическом виде (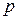 – параметр):
– параметр):
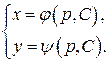
Возможность интегрирования уравнения (4) в квадратурах зависит от того будет ли уравнение (6) интегрироваться в квадратурах. ▲
Замечание. Не следует путать метод введения параметра с методом замены переменной, то есть нельзя после нахождения общего интеграла (7) вместо параметра 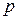 в (7) подставлять
в (7) подставлять 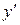 и далее находить
и далее находить 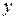 интегрированием, так как равенство (7) есть общий интеграл уравнения (6), которое получено из исходного уравнения (4) не заменой, а дифференцированием его.
интегрированием, так как равенство (7) есть общий интеграл уравнения (6), которое получено из исходного уравнения (4) не заменой, а дифференцированием его.
Аналогичными рассуждениями, используя метод введения параметра, решаются уравнения: 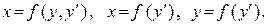
Пример 11. Решить уравнение
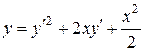 . (10)
. (10)
▲ Данное уравнение вида (4), поэтому для его интегрирования используем метод введения параметра. Обозначим 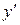 через
через 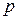 . Подставляя
. Подставляя 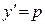 в (10), получим
в (10), получим
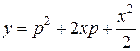 . (11)
. (11)
Дифференцируем (11) по 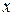 , учитывая, что
, учитывая, что 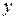 зависит от
зависит от 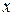 как непосредственно, так и через промежуточную переменную
как непосредственно, так и через промежуточную переменную 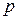 :
:
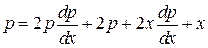 .
.
В результате преобразований приходим к уравнению
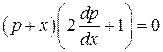 ,
,
которое распадается на два уравнения:
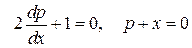 .
.
Общее решение первого уравнения: 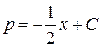 . Подставляя это значение
. Подставляя это значение 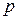
в (11), получаем общее решение исходного уравнения: 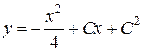 . Из второго уравнения получаем:
. Из второго уравнения получаем: 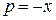 . Если подставить это значение
. Если подставить это значение 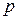 в (11),
в (11),
то получим функцию 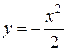 , которая является еще одним решением исходного уравнения, не входящим в его общее решение. ▲
, которая является еще одним решением исходного уравнения, не входящим в его общее решение. ▲
 2015-03-22
2015-03-22 587
587








